题目内容
为了缩短下楼的时间,消防员往往抱着楼房外的竖直杆直接滑下,设消防员先做自由落体运动,再以可能的最大加速度沿杆做匀减速直线运动.一名质量m=65kg的消防员,在沿竖直杆无初速度滑至地面的过程中,重心共下降了h=11.4m,该消防员与杆之间的滑动摩擦力最大可达到fm=975N,消防员着地的速度不能超过v=6m/s.(g=10m/s2)求:
(1)消防员下滑过程中速度的最大值;
(2)消防员下滑过程的最短时间。
(1)消防员下滑过程中速度的最大值;
(2)消防员下滑过程的最短时间。
解:(1)消防队员抱着竖直杆做自由落体运动时,设消防员下滑过程中速度的最大值为vm
则
对消防员匀减速直线运动,设最大加速度的大小为a
则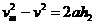
由牛顿第二定律得:
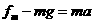
a=5m/s2
由题意:

联立解得:vm=10m/s
(2)对消防员自由下落: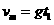
所以t1=1.0s
对消防员匀减速直线运动: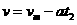
所以t2=0.8s
故消防员下滑过程的最短时间:
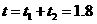 s
s
则

对消防员匀减速直线运动,设最大加速度的大小为a
则
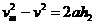
由牛顿第二定律得:
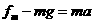
a=5m/s2
由题意:

联立解得:vm=10m/s
(2)对消防员自由下落:
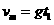
所以t1=1.0s
对消防员匀减速直线运动:
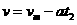
所以t2=0.8s
故消防员下滑过程的最短时间:
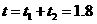 s
s 
练习册系列答案
相关题目
 (2008?虹口区二模)消防队员为了缩短下楼的时间,往往抱着竖直的杆直接滑下.在一次训练中,一名质量为60kg、训练有素的消防队员从离地面18m的高度抱着两端均固定、质量为200kg的竖直杆以最短的时间滑下,要求消防队员落地的速度不能大于6m/s.已知该消防队员对杆作用的最大压力为1800N,他与杆之间的动摩擦因数为0.5,当地的重力加速度为g=10m/s2.求:
(2008?虹口区二模)消防队员为了缩短下楼的时间,往往抱着竖直的杆直接滑下.在一次训练中,一名质量为60kg、训练有素的消防队员从离地面18m的高度抱着两端均固定、质量为200kg的竖直杆以最短的时间滑下,要求消防队员落地的速度不能大于6m/s.已知该消防队员对杆作用的最大压力为1800N,他与杆之间的动摩擦因数为0.5,当地的重力加速度为g=10m/s2.求: 消防队员为了缩短下楼的时间,往往抱着竖直的杆直接滑下.假设一名质量为60kg、训练有素的消防队员从七楼(即离地面18m的高度)抱着竖直的杆以最短的时间滑下.已知杆的质量为200kg,消防队员着地的速度不能大于6m/s,手和腿对杆的最大压力为1800N,手和腿与杆之间的动摩擦因数为0.5.假设杆是搁在地面上的,杆在水平方向不能移动,试在如图所示的坐标图上画出杆对地面的压力随时间变化的图象.
消防队员为了缩短下楼的时间,往往抱着竖直的杆直接滑下.假设一名质量为60kg、训练有素的消防队员从七楼(即离地面18m的高度)抱着竖直的杆以最短的时间滑下.已知杆的质量为200kg,消防队员着地的速度不能大于6m/s,手和腿对杆的最大压力为1800N,手和腿与杆之间的动摩擦因数为0.5.假设杆是搁在地面上的,杆在水平方向不能移动,试在如图所示的坐标图上画出杆对地面的压力随时间变化的图象.