题目内容
 (2008?虹口区二模)消防队员为了缩短下楼的时间,往往抱着竖直的杆直接滑下.在一次训练中,一名质量为60kg、训练有素的消防队员从离地面18m的高度抱着两端均固定、质量为200kg的竖直杆以最短的时间滑下,要求消防队员落地的速度不能大于6m/s.已知该消防队员对杆作用的最大压力为1800N,他与杆之间的动摩擦因数为0.5,当地的重力加速度为g=10m/s2.求:
(2008?虹口区二模)消防队员为了缩短下楼的时间,往往抱着竖直的杆直接滑下.在一次训练中,一名质量为60kg、训练有素的消防队员从离地面18m的高度抱着两端均固定、质量为200kg的竖直杆以最短的时间滑下,要求消防队员落地的速度不能大于6m/s.已知该消防队员对杆作用的最大压力为1800N,他与杆之间的动摩擦因数为0.5,当地的重力加速度为g=10m/s2.求:(1)消防队员下滑过程中的最大速度.
(2)消防队员下滑的最短时间.
(3)请在右图中作出杆对地面的压力随时间变化的图象.
分析:(1)消防队员自由下落的末速度最大,根据自由下落的位移和匀减速直线运动的位移为18m,以及着地速度不超过6m/s,运用运动学公式求出下落的最大速度.
(2)先做自由落体运动,然后以最大加速度做匀减速直线运动,时间最短,根据速度时间公式分别求出自由落体运动时间和匀减速直线运动的时间,从而得出最短时间.
(3)对杆进行受力分析,求出各阶段杆的受力情况,然后作出图象.
(2)先做自由落体运动,然后以最大加速度做匀减速直线运动,时间最短,根据速度时间公式分别求出自由落体运动时间和匀减速直线运动的时间,从而得出最短时间.
(3)对杆进行受力分析,求出各阶段杆的受力情况,然后作出图象.
解答: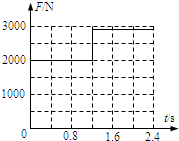 解:消防队员先以最大加速度--重力加速度加速下滑,然后以尽可能大的加速度作减速运动,即运动过程为先加速后减速.当手和腿对杆施加最大压力时(就是抱紧杆的力)其受到的滑动摩擦力最大,此时减速的加速度值为最大.
解:消防队员先以最大加速度--重力加速度加速下滑,然后以尽可能大的加速度作减速运动,即运动过程为先加速后减速.当手和腿对杆施加最大压力时(就是抱紧杆的力)其受到的滑动摩擦力最大,此时减速的加速度值为最大.
(1)最大滑动摩擦力fmax=μN=0.5×1800N=900N,
减速的加速度由牛顿第二定律可知a=
=
5m/s2=5m/s2,
设消防队员加速下滑的距离为h1,减速下滑的距离为(H-h1),
加速阶段的末速度是减速阶段的初速度为υmax,由题意和匀变速运动的规律有:
=2gh1,
=2a(H-h1)+v2,
由此式解得 h1=
=
m=7.2m,
消防队员最大速度为vmax=
=
m/s=12m/s;
(2)加速时间:t1=
=
s=1.2s,
减速时间:t2=
=
s=1.2s,
下滑的时间 t=t1+t2=1.2+1.2=2.4s,
(3)将消防队员与杆作为整体为研究对象时,加速阶段消防队员完全失重,
杆受到地面的支持力等于杆的重力,即N1=Mg=2000N,加速下滑,
消防队员超重,N1=Mg+m(g+a)=2900N.
杆对地面的压力随时间变化图象如图所示.
答:(1)消防队员下滑过程中的最大速度为12m/s.
(2)消防队员下滑的最短时间为2.4s.
(3)杆对地面的压力随时间变化的图象如图所示.
 解:消防队员先以最大加速度--重力加速度加速下滑,然后以尽可能大的加速度作减速运动,即运动过程为先加速后减速.当手和腿对杆施加最大压力时(就是抱紧杆的力)其受到的滑动摩擦力最大,此时减速的加速度值为最大.
解:消防队员先以最大加速度--重力加速度加速下滑,然后以尽可能大的加速度作减速运动,即运动过程为先加速后减速.当手和腿对杆施加最大压力时(就是抱紧杆的力)其受到的滑动摩擦力最大,此时减速的加速度值为最大.(1)最大滑动摩擦力fmax=μN=0.5×1800N=900N,
减速的加速度由牛顿第二定律可知a=
| fmax-mg |
| m |
| 900-600 |
| 60 |
设消防队员加速下滑的距离为h1,减速下滑的距离为(H-h1),
加速阶段的末速度是减速阶段的初速度为υmax,由题意和匀变速运动的规律有:
| v | 2 max |
| v | 2 max |
由此式解得 h1=
| 2aH+v2 |
| 2(g+a) |
| 2×5×18+62 |
| 2×(10+5) |
消防队员最大速度为vmax=
| 2gh1 |
| 2×10×7.2 |
(2)加速时间:t1=
| vmax |
| g |
| 12 |
| 10 |
减速时间:t2=
| vmax-v |
| a |
| 12-6 |
| 5 |
下滑的时间 t=t1+t2=1.2+1.2=2.4s,
(3)将消防队员与杆作为整体为研究对象时,加速阶段消防队员完全失重,
杆受到地面的支持力等于杆的重力,即N1=Mg=2000N,加速下滑,
消防队员超重,N1=Mg+m(g+a)=2900N.
杆对地面的压力随时间变化图象如图所示.
答:(1)消防队员下滑过程中的最大速度为12m/s.
(2)消防队员下滑的最短时间为2.4s.
(3)杆对地面的压力随时间变化的图象如图所示.
点评:分析消防队员的运动过程,应用牛顿第二定律、运动学公式进行分析答题,解决本题的关键搞清消防员的运动过程,知道加速度是处理动力学问题的桥梁.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 (2008?虹口区二模)如图所示是用转动八面镜法测光速的实验示意图,图中S为发光点,T是望远镜,平面镜O与凹面镜B构成了反射系统.八面镜M距反射系统的距离为AB=L(L可长达几十千米),且远大于OB以及S和T到八面镜的距离.现使八面镜转动起来,并缓慢增大其转速,当转动频率(1秒内转过的圈数)达到f0时(可认为是匀速转动),恰能在望远镜中第一次看见发光点S,由此测出光速c.根据题中所测量的物理量得到光速c的表达式正确的是 ( )
(2008?虹口区二模)如图所示是用转动八面镜法测光速的实验示意图,图中S为发光点,T是望远镜,平面镜O与凹面镜B构成了反射系统.八面镜M距反射系统的距离为AB=L(L可长达几十千米),且远大于OB以及S和T到八面镜的距离.现使八面镜转动起来,并缓慢增大其转速,当转动频率(1秒内转过的圈数)达到f0时(可认为是匀速转动),恰能在望远镜中第一次看见发光点S,由此测出光速c.根据题中所测量的物理量得到光速c的表达式正确的是 ( ) (2008?虹口区二模)如图所示为起重机沿竖直方向提起的过程中重物运动的速度-时间图象,则该过程中起重机的输出功率最接近下图中的( )
(2008?虹口区二模)如图所示为起重机沿竖直方向提起的过程中重物运动的速度-时间图象,则该过程中起重机的输出功率最接近下图中的( ) (2008?虹口区二模)如图所示,一列简谐横波沿x轴负方向传播,振幅A=4cm.在t=0时刻,平衡位置相距5cm的两质点a、b的位移分别是2cm、-2cm,它们的运动方向都沿y轴的负方向,据此可以推断( )
(2008?虹口区二模)如图所示,一列简谐横波沿x轴负方向传播,振幅A=4cm.在t=0时刻,平衡位置相距5cm的两质点a、b的位移分别是2cm、-2cm,它们的运动方向都沿y轴的负方向,据此可以推断( )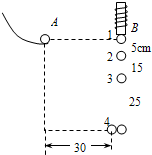 (2008?虹口区二模)如图所示,是利用闪光照相研究平抛运动的示意图,小球A由斜槽滚下,从桌边缘水平抛出,当它恰好离开桌边缘时,小球B也同时下落,闪光频率为10Hz的闪光器拍摄的照片中B球有四个像,像间距离已在图中标出,单位为cm,两球恰在位置4相碰.
(2008?虹口区二模)如图所示,是利用闪光照相研究平抛运动的示意图,小球A由斜槽滚下,从桌边缘水平抛出,当它恰好离开桌边缘时,小球B也同时下落,闪光频率为10Hz的闪光器拍摄的照片中B球有四个像,像间距离已在图中标出,单位为cm,两球恰在位置4相碰.