题目内容
如图所示,光滑水平面上有一静止小车B,左端固定一砂箱,砂箱的右端连接一水平轻弹簧,小车与砂箱的总质量为M1=1.99 kg.车上静置一物体A,其质量为M2=2.00 kg.此时弹簧呈自然长度,物体A的左端的车面是光滑的,而物体A右端的车面与物体间的动摩擦因数为μ=0.2.现有一质量为m=0.01 kg的子弹以水平速度v0=400 m/s打入砂箱且静止在砂箱中,求:
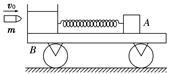
(1)小车在前进过程中,弹簧弹性势能的最大值.
(2)为使物体A不从小车上滑下,车面的粗糙部分至少多长?(g取10 m/s2)

(1)小车在前进过程中,弹簧弹性势能的最大值.
(2)为使物体A不从小车上滑下,车面的粗糙部分至少多长?(g取10 m/s2)
(1)2 J (2)0.5 m
试题分析:(1)子弹射入砂箱后,子弹、砂箱和小车获得共同的速度,设为v1,以子弹、砂箱和小车组成的系统为研究对象,根据动量守恒定律,有
mv0=(M1+m)v1
之后,小车与A通过弹簧作用又达到共同速度,设为v2,此时弹簧压缩最大,则对子
弹、砂箱和小车以及物体、弹簧整个系统,根据动量守恒定律,有
(M1+m)v1=(M1+M2+m)v2
根据能量守恒,有
Ep=
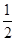 (M1+m)v12-
(M1+m)v12-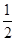 (M1+m+M2)v22
(M1+m+M2)v22联立以上三式得
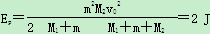 .
.(2)A被压缩的弹簧向右推动直到脱离弹簧后,又通过摩擦力与小车作用再次达到共同
速度,设为v3,对小车与A组成的系统,根据动量守恒定律,有
(M1+M2+m)v2=(M1+M2+m)v3
由此得v2=v3;而对物体A和弹簧组成的系统,根据功能关系,有μM2gs=Ep
解得s=0.5 m.
点评:本题涉及到弹簧,功、机械能守恒的条件、力和运动的关系等较多知识.题目情景比较复杂,全面考查考生理解、分析、解决问题的能力.

练习册系列答案
相关题目

 mgh
mgh 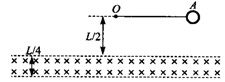
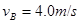 飞出后,恰好能从一倾角为
飞出后,恰好能从一倾角为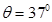 的倾斜传送带顶端C无碰撞的滑上传送带,已知传送带长度为L=2.75m(图中只画出了传送带的部分示意图)物体与传送带之间的动摩擦因数为
的倾斜传送带顶端C无碰撞的滑上传送带,已知传送带长度为L=2.75m(图中只画出了传送带的部分示意图)物体与传送带之间的动摩擦因数为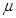 =0.50,(取sin370=0.60,cos370=0.80,g=10m/s2不计空气阻力,不考虑半圆形管AB的内径)
=0.50,(取sin370=0.60,cos370=0.80,g=10m/s2不计空气阻力,不考虑半圆形管AB的内径)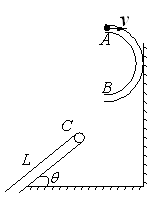
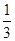 g竖直下落到地面,在此过程中
g竖直下落到地面,在此过程中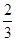 mgh
mgh