题目内容
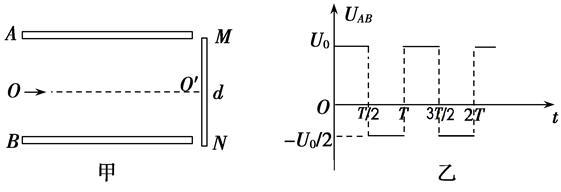
（12分）如图甲所示，M、N为水平放置的平行板电容器的两个极板，两极板间距d=0.1m，两极板间的电压U=12.5V，O为上极板中心的小孔，以O为坐标，在y=0和y=2m之间有沿着x轴方向的匀强电场，PQ为电场区域的上边界，在x轴方向范围足够大，电场强度的变化如图乙所示，取x轴正方向为电场正方向。现有一个带负电的粒子，在t=0时刻从紧靠下级板中心O´处无初速释放，经过小孔O进入交变电场中，粒子的比荷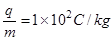
，不计粒子重力.求粒子：（1）进入交变电场时的速度；（2）在8×10-3s末的位置坐标；
（3）离开交变电场时的速度大小和方向。
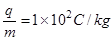，不计粒子重力.求粒子：（1）进入交变电场时的速度；（2）在8×10-3s末的位置坐标；（3）离开交变电场时的速度大小和方向。
（1）50m/s（2）（0.032m,0.2m）（3）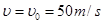
,方向竖直向上。
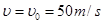,方向竖直向上。试题分析：（1）粒子运动至小孔O的速度为
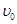，由动能定理得
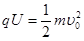2分代入数据得
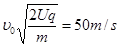2分（2）粒子O´运动至O所用的时间为
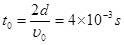1分即自
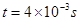开始，粒子垂直射入交变电场，在
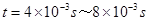内，粒子做类平抛运动在y方向上，粒子做匀速运动，
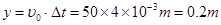1分在x方向上，粒子向右匀加速运动的加速度大小
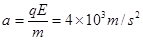1分粒子向右运动的位移
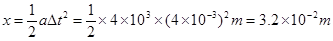1分故粒子在
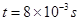末的位置坐标为（0.032m,0.2m）1分（3）由图可知，交变电场的变化周期
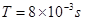,粒子在交变电场中，在y方向上，一直匀速运动；在x方向上，一直向右运动，先匀加速，再匀减速至静止，这样周期性运动下去。 1分
粒子在交变电场中运动的时间
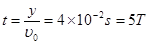1分故粒子离开交变电场时的水平速度为0 1分
因此，粒子离开交变电场时的速度
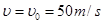,方向竖直向上。1分点评：带电粒子在电场中的运动，综合了静电场和力学的知识，分析方法和力学的分析方法基本相同．先分析受力情况再分析运动状态和运动过程（平衡、加速、减速，直 线或曲线），然后选用恰当的规律解题．解决这类问题的基本方法有两种，第一种利用力和运动的观点，选用牛顿第二定律和运动学公式求解；第二种利用能量转化 的观点，选用动能定理和功能关系求解．
练习册系列答案
相关题目
时刻释放电子，则电子运动的v-t图线如图二所示，该电子一直向着B板匀加速直线运动
时刻释放电子，则电子运动的v-t图如图三所示，该电子在2T时刻在出发点左边
时刻释放电子，在2T时刻电子在出发点的右边
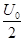，且每隔T/2变向1次。现将质量为m的带正电，且电荷量为q的粒子束从AB的中点O以平行于金属板的方向OO′射入，设粒子能全部打在靶上而且所有粒子在A、B间的飞行时间均为T。不计重力的影响，试问：
