题目内容
【题目】摩天大楼中一部直通高层的客运电梯,行程超过百米.电梯的简化模型如图甲所示.考虑安全、舒适、省时等因素,电梯的加速度a是随时间t变化的.已知电梯在t=0时由静止开始上升,a-t图象如图乙所示.电梯总质量m=2.0×103kg.忽略一切阻力,重力加速度g取10 m/s2.
(1)求电梯在上升过程中受到的最大拉力F1和最小拉力F2;
(2)类比是一种常用的研究方法.对于直线运动,教科书中讲解了由v-t图象求位移的方法.请你借鉴此方法,对比加速度和速度的定义,根据图乙所示的a-t图象,求电梯在第1 s内的速度改变量Δv1和第2 s末的速率v2;
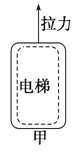
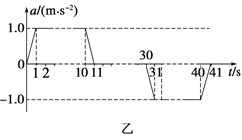
(3)求电梯以最大速率上升时,拉力做功的功率P;再求在0~11 s时间内,拉力和重力对电梯所做的总功W.
【答案】(1)2.2×104N1.8×104N(2)0.5 m/s 1.5 m/s(3)2.0×105W1.0×105J
【解析】试题分析: (1)由牛顿第二定律,有F-mg=ma
由a-t图象可知,F1和F2对应的加速度分别是
a1=1.0 m/s2,a2=-1.0 m/s2,则
F1=m(g+a1)=2.0×103×(10+1.0) N=2.2×104N
F2=m(g+a2)=2.0×103×(10-1.0) N=1.8×104N
(2)类比可得,所求速度变化量等于第1 s内a-t图线与t轴所围图形的面积,可得Δv1=0.5 m/s
同理可得2 s内的速度变化量Δv2=v2-v0=1.5 m/s
v0=0,第2 s末的速率v2=1.5 m/s
(3)由a-t图象可知,11 s~30 s内速率最大,其值vm等于0~11 s内a-t图线与t轴所围图形的面积,此时电梯做匀速运动,拉力F等于重力mg,所求功率P=Fvm=mg·vm=2.0×103×10×10 W=2.0×105W
由动能定理得,总功W=Ek2-Ek1=![]() mvm2-0=
mvm2-0=![]() ×2.0×103×102J=1.0×105J.
×2.0×103×102J=1.0×105J.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】如图所示为探究物体运动加速度与物体质量、物体受力关系的实验装置,砂和砂桶质量用m表示,小车和车上所加砝码总质量用M表示,小车运动加速度用a表示。
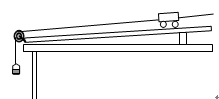
①实验过程中需要适当抬起长木板的一端以平衡小车所受到的摩擦力,该步骤中木板被抬起的角度与小车质量 (选填“有关”或“无关”);
②在探究加速度与小车受力关系过程中, 甲和乙两小组分别用下列两组数据进行实验操作,其中你认为合理的是 (选填“甲”或“乙”);
M甲=500g M乙=500g
甲m(g) | 20 | 22 | 24 | 26 |
乙m(g) | 20 | 30 | 40 | 50 |
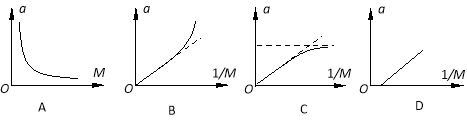
③在探究加速度与小车质量关系过程中,应该保持 不变,通过增减小车中砝码改变小车质量M,实验测出几组a、M数据,下列图线能直观合理且正确反映a-M关系的是 。