Question

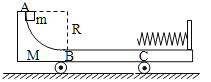
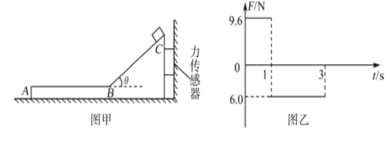
【题目】如图甲所示，在光滑水平面上放置斜面体ABC，水平部分AB与倾斜部分BC平滑连接，AB、BC表面均粗糙，BC与水平面的夹角为．在斜面体右侧与竖直墙壁之间连接着一个力传感器，规定力传感器受压时，其示数为正值，力传感器被拉时，其示数为负值．一个质量m=3 kg可视为质点的滑块从斜面体的C点由静止开始下滑，最终停在AB上某处．在整个运动过程中，ABC始终保持静止，力传感器测得的力F和时间 t的关系如图乙所示．已知sin 37°=0. 6，cos 37°=0.8， g取10 m/s2，求：

（1）滑块与AB的动摩擦因数及滑块到达B点的速度vB；

（2）在整个运动过程中滑块克服摩擦力做的功．

Answer 1

【答案】（1） （2）36J

【解析】

(1)由图象可知，在AB段Ff=6N，t1=2s，对滑块分析，由牛顿第二定律有：

代入数据联立解得： a1=2 m/s2，μ1=0.2， vB=4m/s.

(2)由图象可知，滑块在斜面上运动的时间为t2=1 s，由：

解得a2=4m/s2，当滑块在斜面BC上时，对滑块分析，由牛顿第二定律有：

由图可知斜面对传感器的压力为9.6N，对斜面有：

联立解得μ2=0.25，；滑块在斜面上滑行的距离：

，

解得x=2 m，则滑块克服摩擦力做的功：

解得Wf=36J.