题目内容
【题目】如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点与一条水平轨道相连,轨道都是光滑的.轨道所在空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m的带正电的小球,为使小球刚好在圆轨道内做圆周运动,求释放点A距圆轨道最低点B的距离s.已知小球受到的电场力大小等于小球重力的3/4倍.

【答案】![]()
【解析】
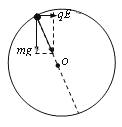
将电场和重力场等效为一个新的重力场,小球刚好沿圆轨道做圆周运动可视为小球到达等效重力场“最高点”时刚好由等效重力提供向心力(如下图所示)可得
![]() (1)
(1)
再对全过程运用动能定理即可求解
![]() (2)
(2)
联立解得:s=![]() R
R
思路将电场和重力场等效为一个新的重力场,小球刚好沿圆轨道做圆周运动可视为小球到达等效重力场“最高点”时刚好由等效重力提供向心力.求出等效重力加速度g′及其方向角,再对全过程运用动能定理即可求解

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目