题目内容
8.如图所示,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点.水平桌面右侧某一位置有一竖直放置的光滑圆弧轨道MNP,且形状为半径R=0.8m的圆环剪去了左上角的135°的圆弧,MN为其竖直直径,P点到桌面的竖直距离也是R.如用质量m1=0.4kg的物块将弹簧缓慢压缩到C点,释放后物块恰停止在B点.用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点,释放后物块过B点后其位移与时间关系为x=6t-2t2(物块飞离后由P点沿切线滑入光滑圆轨道,不计空气阻力,g=10m/s2,求:
(1)物块运动到P点速度的大小和方向.
(2)判断m2能否沿圆轨道到达M点.
(3)释放后m2运动过程中克服摩擦力做的功.
分析 (1)根据物体做平抛运动,根据运动的分解,由运动学公式,即可求解;
(2)根据动能定理与牛顿第二定律,即可求解;
(3)根据能量守恒定律,结合摩擦力做功,即可求解.
解答 解:(1)设物块由D点以初速度vD做平抛运动,落到P点时其竖直速度为:
vy2=2gR
得:vD=vy=4 m/s
所以到P的速度为:vP=4$\sqrt{2}$m/s
方向与水平方向夹角为45°.
(2)若物块能沿轨道到达M点,其速度为vM,根据动能定理,则有:
$\frac{1}{2}$m2v2M=$\frac{1}{2}$m2v2D-$\frac{\sqrt{2}}{2}$m2gR
轨道对物块的压M点.力为FN,则有:
FN+m2g=m2$\frac{{v}_{M}^{2}}{R}$
解得:FN=(1-$\sqrt{2}$)m2g<0
即物块不能到达M点.
(3)设弹簧长为AC时的弹性势能为Ep,物块与桌面间的动摩擦因数为μ,释放m1时,有:Ep=μm1gsCB
释放m2时,有:Ep=μm2gsCB+$\frac{1}{2}$m2v20
代入数据解得:Ep=2.4J
m2在桌面上运动过程中克服摩擦力做功为Wf,则有:
Ep-Wf=$\frac{1}{2}$m2v2D
代入数据可得:Wf=1.6J.
答:(1)物块运动到P点速度的大小4$\sqrt{2}$m/s,方向与水平方向夹角为45°.
(2)m2不能沿圆轨道到达M点.
(3)释放后m2运动过程中克服摩擦力做的功1.6 J.
点评 该题涉及到多个运动过程,既要分析各个过程的规律,同时要把握每个过程之间的联系,运用机械能守恒定律、平抛运动基本公式、圆周运动向心力公式等知识解答.

练习册系列答案
相关题目
19.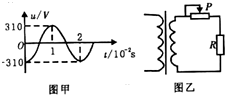 一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头,下列说法正确的是( )
一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头,下列说法正确的是( )
 一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头,下列说法正确的是( )
一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头,下列说法正确的是( )| A. | 副线圈输出电压的有效值为3lV | |
| B. | 副线圈输出电压的频率为50Hz | |
| C. | P向右移动时,原、副线圈的电流都增大 | |
| D. | P向右移动时,变压器的输出功率增加 |
16. 如图所示,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为2m的小球,B处固定质量为m的小球,支架悬挂在O点可绕过O点并与支架所在平面相垂直的固定轴转动.开始时OB与对面相垂直,放手后开始运动,在不计任何阻力的情况下,下列说法正确的是( )
如图所示,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为2m的小球,B处固定质量为m的小球,支架悬挂在O点可绕过O点并与支架所在平面相垂直的固定轴转动.开始时OB与对面相垂直,放手后开始运动,在不计任何阻力的情况下,下列说法正确的是( )
 如图所示,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为2m的小球,B处固定质量为m的小球,支架悬挂在O点可绕过O点并与支架所在平面相垂直的固定轴转动.开始时OB与对面相垂直,放手后开始运动,在不计任何阻力的情况下,下列说法正确的是( )
如图所示,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为2m的小球,B处固定质量为m的小球,支架悬挂在O点可绕过O点并与支架所在平面相垂直的固定轴转动.开始时OB与对面相垂直,放手后开始运动,在不计任何阻力的情况下,下列说法正确的是( )| A. | A球到达最低点时速度为零 | |
| B. | 当支架从右向左摆动时,A球机械能减小量等于B球机械能增加量 | |
| C. | B球向左摆动所能达到的最高位置应等于A球开始运动时的高度 | |
| D. | A球从图示位置向下摆动过程中,支架对A球做负功 |
3.一质量为1kg的质点静止于光滑水平面上,从t=0时起,第1秒受到1N的水平外力作用,第2秒内受到同方向的2N的外力作用,下列判断正确的是( )
| A. | 1s末速度为2m/s | B. | 第1秒内外力的平均功率是0.5W | ||
| C. | 第1.5秒末外力的瞬时功率4W | D. | 0.2s内外力所做的功是4.5J |
13.一质量为1kg的物体从静止开始匀加速竖直下落,经2s落地,落地时的速度大小为18m/s,若重力加速度g取10m/s2,则( )
| A. | 物体的重力势能减少了162J | B. | 物体的动能增加了200J | ||
| C. | 物体的机械能减少了20J | D. | 重力对物体做功180J |
 在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下:
在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下: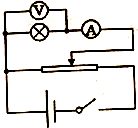 标有“6V,1.5W”的小灯泡,为了测量其0~6V不同电压下的实际功率,提供的器材除导线和开关外,还有:
标有“6V,1.5W”的小灯泡,为了测量其0~6V不同电压下的实际功率,提供的器材除导线和开关外,还有: 如图所示,质量为m的带电小球被绝缘细线系于O点,空间有水平向右、场强大小为E的匀强电场,小球静止时,细绳与竖直方向的夹角为θ,重力加速度为g,求:
如图所示,质量为m的带电小球被绝缘细线系于O点,空间有水平向右、场强大小为E的匀强电场,小球静止时,细绳与竖直方向的夹角为θ,重力加速度为g,求: