��Ŀ����
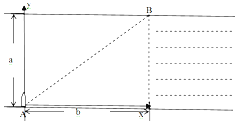
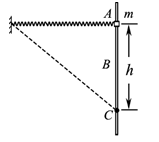
����Ŀ����ͼ��ʾ�����ʵ���һ�˹̶�����һ����һ����Ϊm�����ڴֲ���ֱ�̶���A����Բ������������ˮƽ�Ҵ���ԭ����Բ����A���ɾ�ֹ��ʼ�»�������B�����ٶ������BΪ��AC��ijһ����������C�����ٶ�Ϊ�㣬AC��h�����Բ����C�����һ��ֱ���ϵ��ٶ�v��ǡ���ܻص�A������ʼ���ڵ������ڣ��������ٶ�Ϊg����Բ���� ��
A���»������У��˷�Ħ�������Ĺ�Ϊ![]() mv2
mv2
B���»������У����ٶ�һֱ��С
C����A�»���C�����е��ɵĵ�����������������mgh
D����C�������ɵĵ�������Ϊ![]() mv2��mgh
mv2��mgh
���𰸡�A
��������
���������Բ����A���ɾ�ֹ��ʼ�»�������B�����ٶ������C�����ٶ�Ϊ�㣬����Բ�����������˶������������˶�������B�����ٶ�������Ծ���B���ļ��ٶ�Ϊ�㣬���Լ��ٶ��ȼ�С��������B�����о�Բ����A���ɾ�ֹ��ʼ�»���C���̣����ö��ܶ����г���ʽ![]() ����C�����һ��ֱ���ϵ��ٶ�v��ǡ���ܻص�A�����ö��ܶ����г���ʽ
����C�����һ��ֱ���ϵ��ٶ�v��ǡ���ܻص�A�����ö��ܶ����г���ʽ![]() ����ã�
����ã�![]() ����C�����ɵĵ������ܶ�Ϊ
����C�����ɵĵ������ܶ�Ϊ![]() �����ɵ�����������Ϊ
�����ɵ�����������Ϊ![]() ����A��ȷCD����
����A��ȷCD����

��ϰ��ϵ�д�
�����Ŀ