题目内容
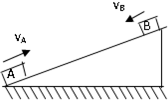 如图所示,一固定斜面长12m,倾角为37°,可视为质点的木块A和B分别置于斜面的顶端和底端,A与B两木块和斜面间的动摩擦因数均为0.5.现用某种弹射作用使它们同时沿斜面相对滑行,滑行的初速vA=10m/s,vB=2m/s.问:经过多长时间A与B两木块相遇?(sin37°=0.6,cos37°=0.8,g=10m/s2)?
如图所示,一固定斜面长12m,倾角为37°,可视为质点的木块A和B分别置于斜面的顶端和底端,A与B两木块和斜面间的动摩擦因数均为0.5.现用某种弹射作用使它们同时沿斜面相对滑行,滑行的初速vA=10m/s,vB=2m/s.问:经过多长时间A与B两木块相遇?(sin37°=0.6,cos37°=0.8,g=10m/s2)?分析:对木块进行受力分析,由牛顿第二定律求出其加速度,由匀变速运动的位移公式求出其位移,当两者相遇时,它们的位移之和等于斜面长度,然后求出物体的运动时间.
解答:解:A上滑时,由牛顿第二定律得:
mgsinθ+μmgcosθ=ma1,
解得:a1=10m/s2,
A、B下滑时:mgsinθ-μmgcosθ=ma2,
解得:a2=2m/s2,
设经t1,A的速度为0,位移为s1,B的位移为s2;
VA=a1t1,
解得t1=1s,s1=
t1=5m,
t1时间内,对B:s2=VBt1+
a2
=3m,
VB,=VB+a2t1=4 m/s,
此时,AB间距离S0=L-s1-s2=4m,
设再经t2B追上A,S0=(VBt +
a2
)-
a2
,
解得t2=1s,
AB相遇的时间:t=t1+t2=2s;
答:经过2s时间A与B两木块相遇.
mgsinθ+μmgcosθ=ma1,
解得:a1=10m/s2,
A、B下滑时:mgsinθ-μmgcosθ=ma2,
解得:a2=2m/s2,
设经t1,A的速度为0,位移为s1,B的位移为s2;
VA=a1t1,
解得t1=1s,s1=
| vA |
| 2 |
t1时间内,对B:s2=VBt1+
| 1 |
| 2 |
| t | 2 1 |
VB,=VB+a2t1=4 m/s,
此时,AB间距离S0=L-s1-s2=4m,
设再经t2B追上A,S0=(VBt +
| 1 |
| 2 |
| t | 2 2 |
| 1 |
| 2 |
| t | 2 2 |
解得t2=1s,
AB相遇的时间:t=t1+t2=2s;
答:经过2s时间A与B两木块相遇.
点评:分析清楚运动过程,应用牛顿第二定律与运动学公式即可正确解题,分析清楚A的运动过程是正确解题的关键.

练习册系列答案
相关题目
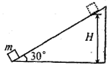 如图所示,一固定斜面的倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g.物块上升的最大高度为H,则此过程中,物块的( )
如图所示,一固定斜面的倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g.物块上升的最大高度为H,则此过程中,物块的( )| A、动能损失了2mgH,机械能损失了mgH | ||
| B、动能损失了mgH,机械能损失了2mgH | ||
C、动能损失了2mgH,机械能损失了
| ||
D、动能损失了mgH,机械能损失了
|
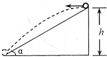 如图所示,一固定斜面的倾角为α,高为h,一小球从斜面顶端沿水平方向抛出,刚好落至斜面底端,不计小球运动中所受的空气阻力,设重力加速度为g,则小球从抛出到落至斜面底端所经历的时间为( )
如图所示,一固定斜面的倾角为α,高为h,一小球从斜面顶端沿水平方向抛出,刚好落至斜面底端,不计小球运动中所受的空气阻力,设重力加速度为g,则小球从抛出到落至斜面底端所经历的时间为( )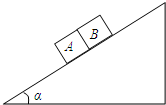 如图所示,一固定斜面上的两个小物块A和B紧挨着匀速下滑,A和B的质量分别为mA=1kg,mB=2kg且A与B的接触面光滑,已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角α=37°,求:
如图所示,一固定斜面上的两个小物块A和B紧挨着匀速下滑,A和B的质量分别为mA=1kg,mB=2kg且A与B的接触面光滑,已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角α=37°,求: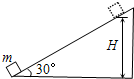 如图所示,一固定斜面倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g.物块上升的最大高度为H,则此过程中,物块的( )
如图所示,一固定斜面倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g.物块上升的最大高度为H,则此过程中,物块的( )