题目内容
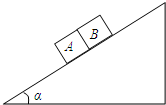 如图所示,一固定斜面上的两个小物块A和B紧挨着匀速下滑,A和B的质量分别为mA=1kg,mB=2kg且A与B的接触面光滑,已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角α=37°,求:
如图所示,一固定斜面上的两个小物块A和B紧挨着匀速下滑,A和B的质量分别为mA=1kg,mB=2kg且A与B的接触面光滑,已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角α=37°,求:(1)A与B之间的弹力是多少
(2)B与斜面之间的动摩擦因数是多少?
分析:先以AB组成的整体为研究对象,根据平衡条件和AB与斜面间的动摩擦因数的关系,求出A、B与斜面间的动摩擦因数,再以A物体为研究对象,根据平衡条件求出B对A的弹力.
解答:解:A、B两物体受到斜面的支持力分别为为NA=mAgcosα,NB=mBgcosα,
所受滑动摩擦力分别为:fA=μAmgcosα,fB=μBmgcosα,
对整体受力分析,根据平衡条件可得
(mB+mA)gsinα=μAmAgcosα+μBmBgcosα,
又由题,μA=2μB,
解之得μB=
tanα=
μA=
再隔离A物体,进行分析研究得
F+mAgsinα=μAmAgcosα
解得 F=3N
答:
(1)A与B之间的弹力是3N.
(2)B与斜面之间的动摩擦因数是μB=
.
所受滑动摩擦力分别为:fA=μAmgcosα,fB=μBmgcosα,
对整体受力分析,根据平衡条件可得
(mB+mA)gsinα=μAmAgcosα+μBmBgcosα,
又由题,μA=2μB,
解之得μB=
| 3 |
| 4 |
| 9 |
| 16 |
| 8 |
| 9 |
再隔离A物体,进行分析研究得
F+mAgsinα=μAmAgcosα
解得 F=3N
答:
(1)A与B之间的弹力是3N.
(2)B与斜面之间的动摩擦因数是μB=
| 9 |
| 16 |
点评:本题是两个物体的平衡问题,首先要选择研究对象,几个相互作用的物体都静止时可能采用整体法和隔离法相结合的方法研究.

练习册系列答案
相关题目
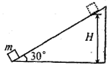 如图所示,一固定斜面的倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g.物块上升的最大高度为H,则此过程中,物块的( )
如图所示,一固定斜面的倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g.物块上升的最大高度为H,则此过程中,物块的( )| A、动能损失了2mgH,机械能损失了mgH | ||
| B、动能损失了mgH,机械能损失了2mgH | ||
C、动能损失了2mgH,机械能损失了
| ||
D、动能损失了mgH,机械能损失了
|
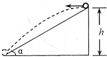 如图所示,一固定斜面的倾角为α,高为h,一小球从斜面顶端沿水平方向抛出,刚好落至斜面底端,不计小球运动中所受的空气阻力,设重力加速度为g,则小球从抛出到落至斜面底端所经历的时间为( )
如图所示,一固定斜面的倾角为α,高为h,一小球从斜面顶端沿水平方向抛出,刚好落至斜面底端,不计小球运动中所受的空气阻力,设重力加速度为g,则小球从抛出到落至斜面底端所经历的时间为( )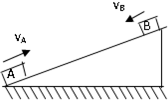 如图所示,一固定斜面长12m,倾角为37°,可视为质点的木块A和B分别置于斜面的顶端和底端,A与B两木块和斜面间的动摩擦因数均为0.5.现用某种弹射作用使它们同时沿斜面相对滑行,滑行的初速vA=10m/s,vB=2m/s.问:经过多长时间A与B两木块相遇?(sin37°=0.6,cos37°=0.8,g=10m/s2)?
如图所示,一固定斜面长12m,倾角为37°,可视为质点的木块A和B分别置于斜面的顶端和底端,A与B两木块和斜面间的动摩擦因数均为0.5.现用某种弹射作用使它们同时沿斜面相对滑行,滑行的初速vA=10m/s,vB=2m/s.问:经过多长时间A与B两木块相遇?(sin37°=0.6,cos37°=0.8,g=10m/s2)?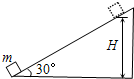 如图所示,一固定斜面倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g.物块上升的最大高度为H,则此过程中,物块的( )
如图所示,一固定斜面倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g.物块上升的最大高度为H,则此过程中,物块的( )