题目内容
6.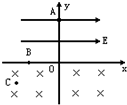 如图所示,在竖直方向的x-y坐标系中,在x轴上方有一个有界的水平向右的匀强电场,场强为E,x轴的下方有一向里的匀强磁场,场强为B.现从电场的上边界上的A点自由释放一个带电量为-q,质量为m的小球,小球从B点进入磁场,到达C点时速度大小为$\frac{mg}{Bq}$,已知A,B点的坐标分别为(0,y0),(-x0,0).求C点的纵坐标y?
如图所示,在竖直方向的x-y坐标系中,在x轴上方有一个有界的水平向右的匀强电场,场强为E,x轴的下方有一向里的匀强磁场,场强为B.现从电场的上边界上的A点自由释放一个带电量为-q,质量为m的小球,小球从B点进入磁场,到达C点时速度大小为$\frac{mg}{Bq}$,已知A,B点的坐标分别为(0,y0),(-x0,0).求C点的纵坐标y?
分析 分析物体在混合场中的运动过程,根据动能定理可求得粒子在磁场中运动的竖直位移,则可求得C点的纵坐标.
解答 解:粒子在混合场中受重力、电场力及洛仑兹力的作用,洛仑兹力不做功;则对动能定理可知:
mgy0+Eqx0+mgy′=$\frac{1}{2}$mv2;
将C点的速度代入可得:
y′=$\frac{{{m^2}g}}{{2{B^2}{q^2}}}-{y_0}-\frac{{Eq{x_0}}}{mg}$
故C点的纵坐标为-y′=$\frac{Eq{x}_{0}}{mg}$+y0-$\frac{{m}^{2}g}{2{B}^{2}{q}^{2}}$
答:C点的纵坐标y为$\frac{Eq{x}_{0}}{mg}$+y0-$\frac{{m}^{2}g}{2{B}^{2}{q}^{2}}$
点评 本题考查带电粒子在复合场中的运动,要注意明确功能关系在粒子运动中的应用;明确洛仑兹力永不做功.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
16. 如图所示,水龙头开口处A的直径d1=2cm,A离地面B的高度h=75cm,当水龙头打开时,从A处流出的水流速度v1=1m/s,在空中形成一完整的水流束.则该水流束在地面B处的截面直径d2约为(g取10m/s2)( )
如图所示,水龙头开口处A的直径d1=2cm,A离地面B的高度h=75cm,当水龙头打开时,从A处流出的水流速度v1=1m/s,在空中形成一完整的水流束.则该水流束在地面B处的截面直径d2约为(g取10m/s2)( )
 如图所示,水龙头开口处A的直径d1=2cm,A离地面B的高度h=75cm,当水龙头打开时,从A处流出的水流速度v1=1m/s,在空中形成一完整的水流束.则该水流束在地面B处的截面直径d2约为(g取10m/s2)( )
如图所示,水龙头开口处A的直径d1=2cm,A离地面B的高度h=75cm,当水龙头打开时,从A处流出的水流速度v1=1m/s,在空中形成一完整的水流束.则该水流束在地面B处的截面直径d2约为(g取10m/s2)( )| A. | 1 cm | B. | 2 cm | ||
| C. | 4 cm | D. | 应大于1 cm,小于2 cm |
1.在静电场中,关于等势面性质,下列说法正确的是( )
| A. | 等势面上各点场强大小一定相等 | |
| B. | 电荷沿等势面移动时,不受电场力作用 | |
| C. | 电荷沿等势面移动时,电场力不做功 | |
| D. | 场强方向总是从电势高的等势面指向电势低的等势面,且与等势面垂直 |
18. 如图所示为杭州乐园的“摩天轮”,它的直径达50米.游人乘坐时,转轮始终不停地匀速转动.关于乘客在乘坐过程中的分析,下列说法中正确的是( )
如图所示为杭州乐园的“摩天轮”,它的直径达50米.游人乘坐时,转轮始终不停地匀速转动.关于乘客在乘坐过程中的分析,下列说法中正确的是( )
 如图所示为杭州乐园的“摩天轮”,它的直径达50米.游人乘坐时,转轮始终不停地匀速转动.关于乘客在乘坐过程中的分析,下列说法中正确的是( )
如图所示为杭州乐园的“摩天轮”,它的直径达50米.游人乘坐时,转轮始终不停地匀速转动.关于乘客在乘坐过程中的分析,下列说法中正确的是( )| A. | 每个乘客都在做加速度为零的匀速运动 | |
| B. | 每个乘客所受的合外力都不等于零 | |
| C. | 每个乘客对座位的压力大小保持不变 | |
| D. | 乘客到达摩天轮的最高点时一定处于“完全失重”状态 |
15.如图所示,是一质点作直线运动的v-t图象,下列说法中正确的是( )


| A. | CD段和DE段的加速度大小相等,方向相反 | |
| B. | 整个过程中,BC段的加速度数值最大 | |
| C. | CE段所表示的运动通过的位移是24m | |
| D. | 整个过程中,质点的运动方向只改变了一次 |
16. 一物块以一定的初速度从斜面底端开始沿粗糙斜面上滑,上升至最高点后又从斜面上滑下,某段时间内物体的v-t图象如图所示.取g=l0m/s2,则( )
一物块以一定的初速度从斜面底端开始沿粗糙斜面上滑,上升至最高点后又从斜面上滑下,某段时间内物体的v-t图象如图所示.取g=l0m/s2,则( )
 一物块以一定的初速度从斜面底端开始沿粗糙斜面上滑,上升至最高点后又从斜面上滑下,某段时间内物体的v-t图象如图所示.取g=l0m/s2,则( )
一物块以一定的初速度从斜面底端开始沿粗糙斜面上滑,上升至最高点后又从斜面上滑下,某段时间内物体的v-t图象如图所示.取g=l0m/s2,则( )| A. | 上升过程中加速度大小为6m/s2 | |
| B. | 下降过程中加速度大小为4m/s2 | |
| C. | 斜面的倾角为30° | |
| D. | 斜面的倾角为37°(sin37°=0.6,cos37°=0.8) |
 某学习小组做探究“合力的功和物体速度变化关系”的实验如图,图中小车是在一条橡皮筋作用下弹出,沿木板滑行至速度最大,这时,橡皮筋对小车做的功记为W.之后用2条、3条…完全相同的橡皮筋并在一起进行第2次、第3次…实验.每次实验中小车获得的速度由打点计时器所打的纸带测出.
某学习小组做探究“合力的功和物体速度变化关系”的实验如图,图中小车是在一条橡皮筋作用下弹出,沿木板滑行至速度最大,这时,橡皮筋对小车做的功记为W.之后用2条、3条…完全相同的橡皮筋并在一起进行第2次、第3次…实验.每次实验中小车获得的速度由打点计时器所打的纸带测出. (1)如图所示,在“研究共点力的合成”实验中,把橡皮筋一端用图钉固定于P点,同时用两个弹簧测力计通过细绳将橡皮筋的另一端拉到位置O,这时除需记录O点位置外,还需记录B和D(用下列选项中的字母表示).
(1)如图所示,在“研究共点力的合成”实验中,把橡皮筋一端用图钉固定于P点,同时用两个弹簧测力计通过细绳将橡皮筋的另一端拉到位置O,这时除需记录O点位置外,还需记录B和D(用下列选项中的字母表示).