Question

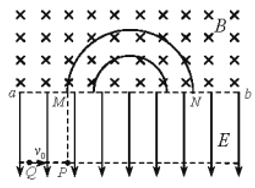
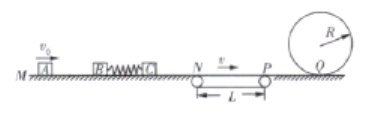
【题目】如图所示为某种游戏装置的示意图，水平轨道MN、PQ分别与水平传送带左侧、右侧理想连接，竖直圆形轨道与PQ相切于Q.已知传送带长，且沿顺时针方向以恒定速率匀速转动两个质量均为m的滑块B、C静置于水平轨道MN上，它们之间有一处于原长的轻弹簧，且弹簧与B连接但不与C连接，另一质量也为m的滑块A以初速度向B运动，A与B碰撞后粘在一起，碰撞时间极短.若C距离N足够远滑块C脱离弹簧后以速度滑上传送带，并恰好停在Q点已知滑块C与传送带及PQ之间的动摩擦因数均为，装置其余部分均视为光滑，重力加速度g取.

（1）求P、Q的距离；

（2）求n0的大小；

（3）若，要使C不脱离竖直圆轨道，求圆轨道半径R的取值范围.

Answer 1

【答案】（1）2.25m（2）3m/s（3）或

【解析】

（1）假设C滑上传送带后一直加速，则

解得

所以假设不成立，C在传送带上一定先加速后匀速，滑上PQ时的速度，又因为C恰好停在Q点，则有

解得：

（2）A与B碰撞，由动量守恒定律得

接下来AB整体压缩弹簧，弹簧恢复原长时，C脱离弹簧，这个过程有

解得

（3）若，A、B碰撞过程中动量守恒，有

AB一起再通过弹簧与C发生作用，有

解得

假设C从N到Q一直减速，有

解得

假设成立，若C恰好到达与圆心等高处，则有

得

即时，C不脱离竖直圆轨道.

若C恰好能通过圆轨道最高点，设C在最高点的速度为，则

解得

则时，C不脱离竖直圆轨道

综上，圆轨道半径R的取值范围为或