Question

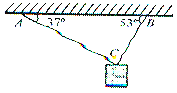
【题目】如图所示，一物体M从A点以某一初速度沿倾角α=30°的粗糙固定斜面向上运动，自顶端B点飞出后，垂直撞到高H=1.95m的竖直墙面上C点，又沿原轨迹返回.已知B、C两点的高度差h=0.45m，物体M与斜面间的动摩擦因数μ=，重力加速度g=10m/s.试求：

(1)物体M沿斜面向上运动时的加速度大小；

(2)物体返回后B点时的速度；

(3)物体被墙面弹回后，从B点回到A点所需的时间.

Answer 1

【答案】(1) （2） 方向沿斜面向下（3） 或

【解析】解：(1)物体M沿斜面向上运动时的加速度为a，由牛顿第二定律有：

mgsinθ+μmgcosθ=ma

代入数据得： a=8m/s

(2)物体从C点到B点做平抛运动，设落至B点时在竖直方向的速度为，

由平抛运动规律有：

代入数据得： =3m/s

由题意知，物体落在B点后刚好沿斜而下滑，则它落至B点时的速度方向沿斜

面向下，与水平方向的夹角为30°

大小为：

方向沿斜面向下

(3)设物体从B点返回到A 点过程中的加速度大小为a′.时间为t′，由牛顿第二定律得：

Mgsinθ-μmgcosθ=ma′

代入数据得： a′=2m/s

由运动学公式有：

代入数据得： s或0.46s