题目内容
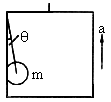
电梯以加速度a=0.6g从静止由地面开始向上做匀加速直线运动,内有用细绳吊着的小球距电梯的地板2m,电梯向上运动了2s,绳突然断了,小球落到地板上需要的时间为
0.5
0.5
s,当小球恰好落到地板上时,小球离地面的高度是18.75
18.75
m.分析:绳子断裂后,小球做竖直上抛运动,结合小球的位移和电梯的位移关系,求出小球落到地面的时间,求出小球的位移,抓住电梯的位移,得出小球离地面的高度.
解答:解:绳子断裂时,小球的速度v0=at=0.6×10×2m/s=12m/s,方向竖直向上.
设经过t时间小球落到地板上.
则v0t+
at2-(v0t-
gt)2=2m
解得t=0.5s.
在此过程中,小球上升的位移x1=v0t-
gt2=12×0.5-5×0.25m=4.75m.
开始电梯上升的位移x2=
at12=
×6×4m=12m
则h=x1+x2+2m=18.85m.
故答案为:0.5s 18.75m.
设经过t时间小球落到地板上.
则v0t+
| 1 |
| 2 |
| 1 |
| 2 |
解得t=0.5s.
在此过程中,小球上升的位移x1=v0t-
| 1 |
| 2 |
开始电梯上升的位移x2=
| 1 |
| 2 |
| 1 |
| 2 |
则h=x1+x2+2m=18.85m.
故答案为:0.5s 18.75m.
点评:解决本题的关键掌握竖直上抛运动的规律,结合运动学公式灵活求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
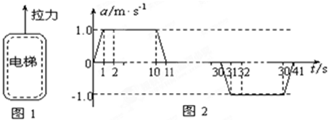 摩天大楼中一部直通高层的客运电梯.行程超过百米.电梯的简化模型如下所示.电梯的加速度a随时间t变化的.已知电梯在t=0时由静止开始上升,a一t图象如图2所示.电梯总质最m=2.0x103kg.忽略一切阻力.重力加速度g取10m/s2.求
摩天大楼中一部直通高层的客运电梯.行程超过百米.电梯的简化模型如下所示.电梯的加速度a随时间t变化的.已知电梯在t=0时由静止开始上升,a一t图象如图2所示.电梯总质最m=2.0x103kg.忽略一切阻力.重力加速度g取10m/s2.求 上海环球金融中心中一部直通高层的电梯,行程超过百米.电梯的简化模型如图1所示.考虑安全、舒适、省时等因素,电梯的加速度a随时间t变化的.已知电梯在t=0时由静止开始上升,a-t图如图2所示.电梯总质量m=2.0×103kg.忽略一切阻力,重力加速度g取10m/s2.
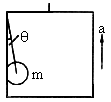
上海环球金融中心中一部直通高层的电梯,行程超过百米.电梯的简化模型如图1所示.考虑安全、舒适、省时等因素,电梯的加速度a随时间t变化的.已知电梯在t=0时由静止开始上升,a-t图如图2所示.电梯总质量m=2.0×103kg.忽略一切阻力,重力加速度g取10m/s2.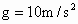 )
)
 )
)