题目内容
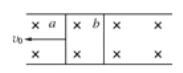
【题目】一个质量为m1的人造地球卫星在高空做匀速圆周运动，轨道半径为r。某时刻和一个质量为m2的同轨道反向运动的太空碎片发生迎面正碰，碰后二者结合成一个整体，并开始沿椭圆轨道运动，轨道的远地点为碰撞时的点。若碰后卫星的内部装置仍能有效运转，当卫星与碎片的整体再次经过远地点时，通过极短时间喷气可使整体仍在卫星碰前的轨道上做圆周运动，绕行方向与碰前相同。已知地球的半径为R，地球表面的重力加速度大小为g，下列说法正确的是（ ）
A. 卫星与碎片碰撞前的线速度大小为
B. 卫星与碎片碰撞前运行的周期大小为
C. 喷气装置对卫星和碎片整体所做的功为
D. 喷气装置对卫星和碎片整体所做的功为
【答案】BC
【解析】试题分析：据万有引力提供圆周运动向心力，即可求出卫星与碎片碰撞前的线速度大小与周期的大小；由动量守恒定律和动能定理即可求出喷气装置对卫星和碎片整体所做的功．
卫星圆周运动的向心力由万有引力提供可得
，又
，可得
，故A错误；据万有引力提供圆周运动向心力，有
解得卫星周期为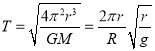
，故B正确；根据动量守恒定律可得： 
，由动能定理可得
，喷气装置对卫星和碎片整体所做的功为
．故C正确D错误．
练习册系列答案
名校课堂系列答案
相关题目
