题目内容
如图8-55所示,半径为r,质量不计的圆盘盘面与地面垂直,圆心处有一个垂直盘面的光滑水平定轴O,在盘的右边缘固定
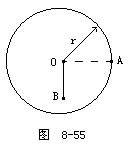
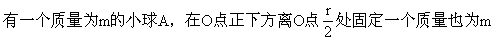
的小球B,放开盘让其自由转动.问:
(1)当A转到最低点时,两小球的重力势能之和减少了多少?
(2)A球转到最低点时的线速度是多少?
(3)在转动过程中半径OA向左偏离竖直方向的最大角度是多少?

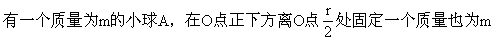
的小球B,放开盘让其自由转动.问:
(1)当A转到最低点时,两小球的重力势能之和减少了多少?
(2)A球转到最低点时的线速度是多少?
(3)在转动过程中半径OA向左偏离竖直方向的最大角度是多少?
(1)两球重力势能之和减少了
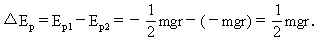
(2)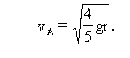
(3)设半径OA向左偏离竖直线的最大角度为θ,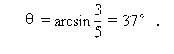
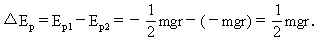
(2)
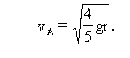
(3)设半径OA向左偏离竖直线的最大角度为θ,
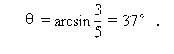
两小球重力势能之和的减少,可选取任意参考平面为零势能参考平面进行计算.由于圆盘转动过程中,只有两小球重力做功,根据机械能守恒定律可列式算出A球的线速度和半径OA的最大偏角.
(1)以通过转轴O的水平面为零势能面,开始时两球重力势能之和为
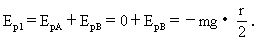
当A球转至最低点时两球重力势能之和为
Ep2=EpA+EpB=-mgr+0=-mgr,
故两球重力势能之和减少了
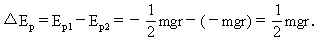
(2)由于圆盘转动过程中,只有两球重力做功,机械能守恒,因此两球重力势能之和的减少一定等于两球动能的增加,设A球转至最低点,A、B两球的线速度分别为vA,vB,则
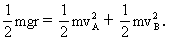
因A、B两球固定在同一圆盘上,转动过程中的角速度ω相同.由
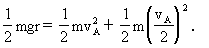
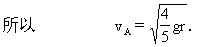
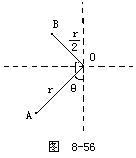
(3)设半径OA向左偏离竖直线的最大角度为θ,如图8-56,该位置系统的机械能与开始时的机械能分别为
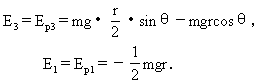
由系统机械能守恒定律E1=E3,即
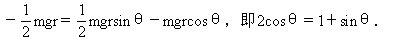
两边平方得 4(1-sin2θ)=1+sin2θ+2sinθ,
所以 5sin2θ+2sinθ-3=0,
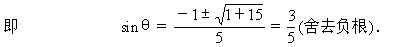
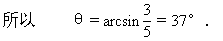
[小结] 系统的始态、末态的重力势能,因参考平面的选取会有所不同,但是重力势能的变化却是绝对的,不会因参考平面的选取而异.机械能守恒的表达方式可以记为
Ek1+Ep1=Ek2+Ep2,
也可以写作:ΔEk增=ΔEp减.本题采用的就是这种形式.
(1)以通过转轴O的水平面为零势能面,开始时两球重力势能之和为
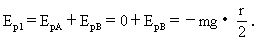
当A球转至最低点时两球重力势能之和为
Ep2=EpA+EpB=-mgr+0=-mgr,
故两球重力势能之和减少了
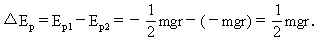
(2)由于圆盘转动过程中,只有两球重力做功,机械能守恒,因此两球重力势能之和的减少一定等于两球动能的增加,设A球转至最低点,A、B两球的线速度分别为vA,vB,则
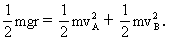
因A、B两球固定在同一圆盘上,转动过程中的角速度ω相同.由

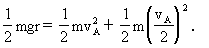
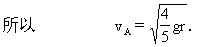
(3)设半径OA向左偏离竖直线的最大角度为θ,如图8-56,该位置系统的机械能与开始时的机械能分别为

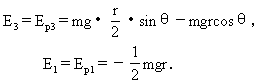
由系统机械能守恒定律E1=E3,即
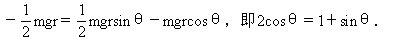
两边平方得 4(1-sin2θ)=1+sin2θ+2sinθ,
所以 5sin2θ+2sinθ-3=0,
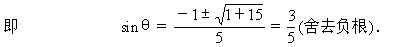
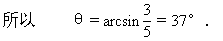
[小结] 系统的始态、末态的重力势能,因参考平面的选取会有所不同,但是重力势能的变化却是绝对的,不会因参考平面的选取而异.机械能守恒的表达方式可以记为
Ek1+Ep1=Ek2+Ep2,
也可以写作:ΔEk增=ΔEp减.本题采用的就是这种形式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的瞬时冲量,则物块在车上滑行的路程s=?。(设物块与车挡板碰撞时没有能量损失)
的瞬时冲量,则物块在车上滑行的路程s=?。(设物块与车挡板碰撞时没有能量损失)
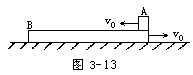 放一质量为m的小木块A,m<M。现以地面为参考系,给A和B以大小相同,方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板。求小木块A向左运动到达最远处(对地)离出发点的距离。
放一质量为m的小木块A,m<M。现以地面为参考系,给A和B以大小相同,方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板。求小木块A向左运动到达最远处(对地)离出发点的距离。

 ,重力加速度用g表示,滑块从A处到达B处时m和M组成的系统动能增加量可表示为ΔEk=,系统的重力势能减少量可表示为ΔEp=,在误差允许的范围内,若ΔEk = ΔEp则可认为系统的机械能守恒;
,重力加速度用g表示,滑块从A处到达B处时m和M组成的系统动能增加量可表示为ΔEk=,系统的重力势能减少量可表示为ΔEp=,在误差允许的范围内,若ΔEk = ΔEp则可认为系统的机械能守恒; 图象如图所示,并测得M=m,则重力加速度g=m/s2。
图象如图所示,并测得M=m,则重力加速度g=m/s2。