题目内容
【题目】如图所示，圆柱形的仓库内有三块长度不同的滑板aO、bO、cO，其下端都固定于底部圆心O，而上端则搁在仓库侧壁上，三块滑板与水平面的夹角依次是30°、45°、60°．若有三个小孩同时从a、b、c处开始下滑（忽略阻力）则（ ）
A. a处小孩最先到O点
B. b处小孩最后到O点
C. c处小孩最先到O点
D. a、c处小孩同时到O点
【答案】D
【解析】试题分析：根据牛顿第二定律和匀变速直线运动规律，分别计算出小孩从a、b、c三块滑板到O所用的时间进行比较即可．
解：斜面上的加速度：a=
=gsinθ
斜面的长度s=
根据匀变速直线运动规律s=
at2
得：gsinθt2=
t2=
=
=
=
=
=
=
＜
=
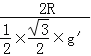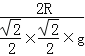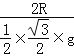tb＜ta=tc，
即b先到，ac同时到
故选：D
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
