题目内容
在坐标系xOy平面的第一象限内，有一个匀强磁场，磁感应强度大小恒为B0，方向垂直于xOy平面，且随时间作周期性变化，如图所示，规定垂直xOy平面向里的磁场方向为正。一个质量为m，电荷量为q的正粒子，在t=0时刻从坐标原点以初速度v0沿x轴正方向射入，不计重力的影响，经过一个磁场变化周期T（未确定）的时间，粒子到达第Ⅰ象限内的某点P，且速度方向仍与x轴正方向平行同向。则
（1）粒子进入磁场后做圆周运动的半径是多大？
（2）若O、P连线与x轴之间的夹角为45°，则磁场变化的周期T为多大？
（3）因P点的位置随着磁场周期的变化而变化，试求P点的纵坐标的最大值为多少？
（1）
（2）T=
（3）ym=（2+）
解析:
（1）粒子进入磁场后做圆周运动的轨道半径为r
（2分） ∴
（2分）
（2）O、P连线与x轴之间的夹角为45°，由运动的对称性，粒子经两个四分之一圆弧到达P点，设圆周运动周期为T0，由T0=
，得 T0=
∴T= =
（4分）
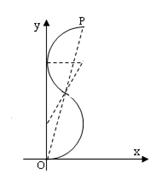（3）设两段圆弧的圆心OO的连线与y轴夹角为θ，P点的纵坐标为y，圆心O到y轴之间的距离为x，则由几何关系，得
y=2r+2rcosθ （2分）
sinθ= （2分）
保证粒子在第一象限内运动，
x≥r （2分）
当θ=300时，y取最大，
ym=（2+）
（2分）
练习册系列答案
相关题目
（2011?福建模拟）如图所示，在坐标系xoy平面的x＞0区域内，有电场强度E=2×105N/C，方向沿y轴负向的匀强电场和磁感应强度B=0.20T，方向与xoy平面垂直向里的匀强磁场．在y轴上有一足够长的荧光屏MN，在x轴上的P（10，0）点处有一粒子发射枪连续不断的发射大量质量m=6.4×10-27kg，电量q=3.2×10-19C的带正电粒子，其向x轴方向发射的粒子恰能沿x轴做匀速直线运动．若撤去电场，并使粒子发射枪以P为轴在xoy平面内以角速度ω=2πrad/s逆时针转动（整个装置都处在真空中），求：
