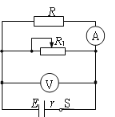
题目内容
【题目】如图所示,一足够长的固定斜面倾角![]() ,两物块A、B的质量
,两物块A、B的质量![]() 、
、![]() 分别为1kg和2kg,它们与斜面之间的动摩擦因数均为
分别为1kg和2kg,它们与斜面之间的动摩擦因数均为![]() 两物块之间的轻绳长
两物块之间的轻绳长![]() ,作用在B上沿斜面向上的力F逐渐增大,使A、B一起由静止开始沿斜面向上运动,g取
,作用在B上沿斜面向上的力F逐渐增大,使A、B一起由静止开始沿斜面向上运动,g取![]()
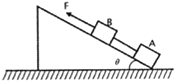
(1)当作用在物块B桑的拉力F达到42N时,连接物块A、B之间的轻绳恰好被拉断,求该轻绳能承受的最大拉力;
(2)若连接物块A、B之间的轻绳恰好被拉断瞬间A、B的速度均为![]() ,轻绳断裂后作用在B物块上的外力
,轻绳断裂后作用在B物块上的外力![]() 不变,求当A运动到最高点时,物块A、B之间的距离。
不变,求当A运动到最高点时,物块A、B之间的距离。
【答案】(1) 14N (2) 11m
【解析】
(1)对整体,根据牛顿第二定律求出加速度大小,再隔离对B分析,根据牛顿第二定律求出绳子的承受力.
(2)根据牛顿第二定律求出绳断后A、B的加速度,结合速度时间公式求出A速度减为零的时间,从而求出这段时间内A、B的位移,根据位移关系求出A、B间的距离.
(1)对AB整体受力分析,由牛顿第二定律得:
![]()
代入数据解得:![]()
对B物体受力分析,由牛顿第二定律得:![]()
代入数据解得:![]()
![]() 细线断裂后,对A物体受力分析,由牛顿第二定律得:
细线断裂后,对A物体受力分析,由牛顿第二定律得:![]()
代入数据解得:![]()
由运动学公式有:![]()
解得:![]()
由运动学有:![]()
细线断裂后,对B物体受力分析,由牛顿第二定律得:![]()
代入数据解得:![]()
由运动学公式有:![]()
代入数据解得:![]()
由题意可知,当A运动到最高点时,物体AB间的距离为:![]()

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目