题目内容
【题目】如图所示,一个足够大的水池盛满清水,水深h=4m,水池底部中心有一点光源A,其中一条光线斜射到水面上距A为l=5m的B点时,它的反射光线与折射光线恰好垂直.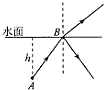
(1)求水的折射率n;
(2)用折射率n和水深h表示水面上被光源照亮部分的面积(圆周率用π表示).
【答案】
(1)
解:设射向B点的光线入射角与折射角分别i和r,
由题意得 sini= ![]() =
= ![]() =0.6,i=37°
=0.6,i=37°
i+r=90°
则 r=53°
故水的折射率为 n= ![]() =
= ![]() =
= ![]() ≈1.33
≈1.33
(2)
解:设射向水面的光发生全反射的临界角为C
则有 sinC= ![]()
圆形光斑的半径为 R=htanC
圆形光斑的面积为 S=πR2
联立可解得 S= ![]()
【解析】(1)由几何关系求出入射角,结合反射光线与折射光线恰好垂直,求出折射角,再根据折射定律求解水的折射率;(2)当光恰好发生全反射,亮斑面积最大,由sinC= ![]() 可求出临界角,再由几何关系,可求出水面上被光源照亮部分的面积.
可求出临界角,再由几何关系,可求出水面上被光源照亮部分的面积.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目