题目内容
两个质量分别为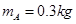
、
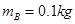的小滑块A、B和一根轻质短弹簧，弹簧的一端与小滑块A粘连，另一端与小滑块B接触而不粘连.现使小滑块A和B之间夹着被压缩的轻质弹簧，处于锁定状态，一起以速度
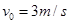在水平面上做匀速直线运动，如题8图所示.一段时间后，突然解除锁定（解除锁定没有机械能损失），两滑块仍沿水平面做直线运动，两滑块在水平面分离后，小滑块B冲上斜面的高度为
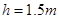.斜面倾角
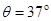，小滑块与斜面间的动摩擦因数为
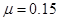，水平面与斜面圆滑连接.重力加速度
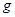取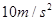
.求：（提示：
，
）
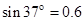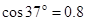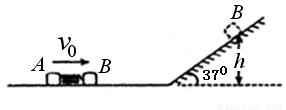
（1）A、B滑块分离时，B滑块的速度大小.
（2）解除锁定前弹簧的弹性势能.
【答案】
（1）
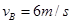（2）
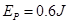
【解析】
试题分析：（1）设分离时A、B的速度分别为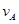
、
，
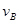小滑块B冲上斜面轨道过程中，由动能定理有：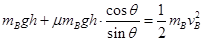
① （3分）
代入已知数据解得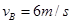： ② （2分）
（2）由动量守恒定律得：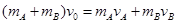
③ （3分）
解得：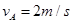
（2分）
由能量守恒得：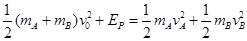
④ （4分）
解得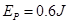： ⑤ （2分）
考点：本题考查了动能定理、动量守恒定律、能量守恒定律.
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
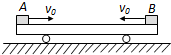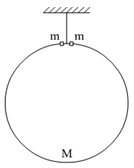
质量为M=4.0kg的平板小车静止在光滑的水平面上，如图所示，当t=0时，两个质量分别为mA=2kg、mB=1kg的小物体A、B都以大小为v0=7m/s．方向相反的水平速度，同时从小车板面上的左右两端相向滑动．到它们在小车上停止滑动时，没有相碰，A、B与车间的动摩擦因素μ=0.2，取g=10m/s2，求：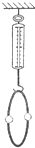
如图所示，弹簧秤下悬挂一质量为M的圆环，环上有两个质量均为m的小环自大环顶部开始分别向两边滑下，当两个小环下落至与大环圆心等高时，每个小环所受摩擦力均为f，则此时弹簧秤示数为（ ）
