题目内容
(选修模块3-5)(1)某些放射性元素如
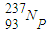 的半衰期很短,在自然界很难被发现,可以在实验室使用人工的方法发现.已知
的半衰期很短,在自然界很难被发现,可以在实验室使用人工的方法发现.已知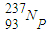 经过一系列α衰变和β衰变后变成
经过一系列α衰变和β衰变后变成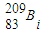 ,下列说法正确的是______
,下列说法正确的是______A.
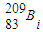 的原子核比
的原子核比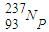 的原子核少28个中子
的原子核少28个中子B.衰变过程中共发生了4次α衰变和7次β衰变
C.衰变过程中共有4个中子转变为质子
D.若
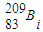 继续衰变成新核
继续衰变成新核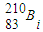 ,需放出一个α粒子
,需放出一个α粒子(2)爱因斯坦提出了光量子概念,并成功地解释光电效应的规律而获得1921年的诺贝尔物理学奖.已知用频率为γ的某种光照射某种金属逸出光电子的最大速度为vm,设光电子的质量为m,则该金属的逸出功为______m

【答案】分析:(1)正确解答本题需要掌握:电荷数、质子数以及质量数之间的关系;能正确根据质量数和电荷数守恒判断发生α和β衰变的次数.
(2)根据光电效应方程EKm=hγ-hγ求出光电子的最大初动能,逸出功与入射光的频率无关,由本身的性质决定.
(3)A与B相互作用过程中,外力的合力为零,系统动量守恒;
解答:解:(1)A、83209Bi的原子核比93237Np少10个质子,质子数和中子数总共少28,故83209Bi的原子核比93237Np少18个中子,故A错误;
B、设83209Bi变为93237Np需要经过x次α衰变和y次β衰变,根据质量数和电荷数守恒则有:93=2x-y+83,4x=237-209,所以解得:x=7,y=4,故B错误,
C、4次β衰变,所以衰变过程中共有4个中子转变为质子,故C正确;
D、若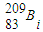 继续衰变成新核
继续衰变成新核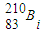 ,需放出一个中子,故D错误
,需放出一个中子,故D错误
故选C.
(2)根据光电效应方程EKm=hγ-W
所以该金属的逸出功为W=hγ-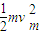
若将入射光的频率提高到2γ,则逸出光电子的最大初动能大于原来初动能的2倍.
(3)①以向左为正方向,根据动量守恒定律
m2v2-m1v1=m2vB.
解得vB=2m/s
②两滑块相距最近时,AB速度相同
m2v2-m1v1=(m1+m2)v′B
v′B= m/s
m/s
故答案为:(1)C
(2)hγ-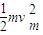 ,大于
,大于
(3)①当滑块A的速度减为0时,滑块B的速度大小是2m/s;
②两滑块相距最近时滑块B的速度大小是 m/s.
m/s.
点评:(1)本题考查了原子核衰变过程中质量数和电荷数守恒的应用,对于这一重点知识,要注意加强练习.
(2)解决本题的关键掌握光电效应方程EKm=hγ-W,以及知道逸出功W=hγ.
(3)本题关键对两物体的受力情况和运动情况进行分析,然后根据动量守恒定律求解
(2)根据光电效应方程EKm=hγ-hγ求出光电子的最大初动能,逸出功与入射光的频率无关,由本身的性质决定.
(3)A与B相互作用过程中,外力的合力为零,系统动量守恒;
解答:解:(1)A、83209Bi的原子核比93237Np少10个质子,质子数和中子数总共少28,故83209Bi的原子核比93237Np少18个中子,故A错误;
B、设83209Bi变为93237Np需要经过x次α衰变和y次β衰变,根据质量数和电荷数守恒则有:93=2x-y+83,4x=237-209,所以解得:x=7,y=4,故B错误,
C、4次β衰变,所以衰变过程中共有4个中子转变为质子,故C正确;
D、若
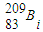 继续衰变成新核
继续衰变成新核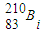 ,需放出一个中子,故D错误
,需放出一个中子,故D错误故选C.
(2)根据光电效应方程EKm=hγ-W
所以该金属的逸出功为W=hγ-
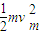
若将入射光的频率提高到2γ,则逸出光电子的最大初动能大于原来初动能的2倍.
(3)①以向左为正方向,根据动量守恒定律
m2v2-m1v1=m2vB.
解得vB=2m/s
②两滑块相距最近时,AB速度相同
m2v2-m1v1=(m1+m2)v′B
v′B=
 m/s
m/s故答案为:(1)C
(2)hγ-
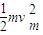 ,大于
,大于(3)①当滑块A的速度减为0时,滑块B的速度大小是2m/s;
②两滑块相距最近时滑块B的速度大小是
 m/s.
m/s.点评:(1)本题考查了原子核衰变过程中质量数和电荷数守恒的应用,对于这一重点知识,要注意加强练习.
(2)解决本题的关键掌握光电效应方程EKm=hγ-W,以及知道逸出功W=hγ.
(3)本题关键对两物体的受力情况和运动情况进行分析,然后根据动量守恒定律求解

练习册系列答案
相关题目