题目内容
如图所示，Ⅰ、Ⅱ、Ⅲ为电场和磁场的理想边界，一束电子（电量为e，质量为m，重力不计）由静止状态从P点经过Ⅰ、Ⅱ间的电场加速后垂直到达边界Ⅱ的Q点。匀强磁场的磁感应强度为B，磁场边界宽度为d，电子从磁场边界Ⅲ穿出时的速度方向与电子原来的入射方向夹角为30°。求：
（1）电子在磁场中运动的时间t；
（2）若改变PQ间的电势差，使电子刚好不能从边界Ⅲ射出，则此时PQ间的电势差U是多少？
（1）电子在磁场中运动的时间t；
（2）若改变PQ间的电势差，使电子刚好不能从边界Ⅲ射出，则此时PQ间的电势差U是多少？
（1）
（2）
（2）试题分析：（1）电子进入磁场后做匀速圆周运动，
设其半径为R，则 evB=
电子在磁场的周期为
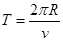，于是得电子在磁场中运动周期
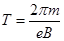
电子在磁场中的轨迹如图，由几何关系得：
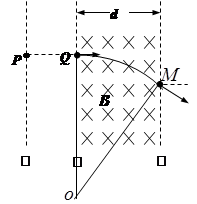
联立以上各式得电子在磁场中运动时间t=
=
所以t=
（2）电子刚好不从边界Ⅲ穿出时，说明电子在磁场中做匀速圆周运动的轨迹恰好与区域的右边界相切，画出电子的运动轨迹如图所示，运动半径为R=d
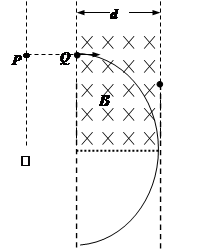
设电子在PQ间被加速电场加速后速度为
，据动能定理有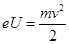 
电子在磁场中做匀速圆周运动，洛伦兹力提供向心力，根据牛顿第二定律得：evB=
以上三式联立解得
练习册系列答案
相关题目
点.若在直角坐标系xOy的第一象限区域内，加上方向沿y轴正方向、大小为E=Bv0的匀强电场，在x=3a处垂直于x轴放置一平面荧光屏，与x轴交点为Q.忽略电子间的相互作用，不计电子的重力.试求：
圆弧导轨，O、P连线水平，M、N与E、F在同一水平高度，水平和圆弧导轨电阻不计，在其上端连有一阻值为R=8W的电阻，在PQ左侧有处于竖直向上的有界匀强磁场，磁感应强度大小为B0=6T。现有一根长度稍大于L、质量为m=0.2kg、电阻为r=2W的金属棒从轨道的顶端P处由静止开始下滑，到达轨道底端MN时对轨道的压力为2mg，取g=10m/s2，求：
=50cm。导轨处在垂直纸面向里的磁感应强度B=5T的匀强磁场中。一根电阻r=0.1Ω的金属棒ab可紧贴导轨左右运动。两块平行的、相距d=10cm、长度L=20cm的水平放置的金属板A和C分别与两平行导轨相连接，图中跨接在两导轨间的电阻R=0.4Ω，其余电阻忽略不计。已知当金属棒ab不动时，质量m=10g、带电量
的小球以某一速度
沿金属板A和C的中线射入板间，恰能射出金属板（g取10m/s2）。求：
