题目内容
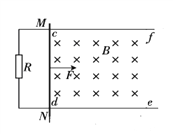
【题目】如图所示,光滑的平行金属导轨水平放置,电阻不计,导轨间距为L,左侧接一阻值为R的电阻。区域cdef内存在垂直轨道平面向下的磁感应强度为B的匀强磁场。质量为m、电阻为r的导体棒MN垂直于导轨放置,并与导轨接触良好。棒MN在平行于轨道的水平拉力作用下,由静止开始做加速度为a匀加速度直线运动运动并开始计时,求:
(1)棒位移为s时的速度及此时MN两端的电压;
(2)棒运动时间t内通过电阻R的电量;
(3)棒在磁场中运动过程中拉力F与时间t的关系;
(4)若撤去拉力后,棒的速度随位移s的变化规律满足v=v0-cs,(c为已知的常数),撤去拉力后棒在磁场中运动距离为d时恰好静止,则拉力作用的时间为多少?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】(1)棒静止开始匀加速度直线运动v12=2as
![]()
E=BLv1, ![]() ,
, ![]()
(2)![]() ,I随时间均匀变化
,I随时间均匀变化![]()
(3)t时刻,导体运动速度为![]()
所以安培力![]()
对棒受力分析,由牛顿第二定律得F合=ma
![]() ,所以拉力与时间关系为
,所以拉力与时间关系为![]()
(4)设拉力作用的时间为t0,则v0=at0
当位移为d时速度v=0代入v=v0-cs得![]()

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目