Question

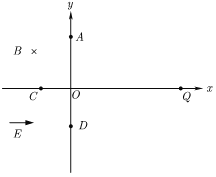
【题目】如图，在坐标系xOy的第二象限存在匀强磁场，磁场方向垂直于xOy平面向里；第三象限内有沿x轴正方向的匀强电场；第四象限的某圆形区域内存在一垂直于xOy平面向里的匀强磁场，磁感应强度大小为第二象限磁场磁感应强度的4倍。一质量为m、带电荷量为q（q>0）的粒子以速率v自y轴的A点斜射入磁场，经x轴上的C点以沿y轴负方向的速度进入电场，然后从y轴负半轴上的D点射出，最后粒子以沿着y轴正方向的速度经过x轴上的Q点。已知OA=，OC=d，OD=，OQ=4d，不计粒子重力。

（1）求第二象限磁感应强度B的大小与第三象限电场强度E的大小；

（2）求粒子由A至D过程所用的时间；

（3）试求第四象限圆形磁场区域的最小面积。

Answer 1

【答案】（1），（2）（3）

【解析】

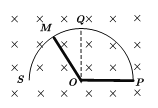
(1)由题意画出粒子轨迹图如图所示：

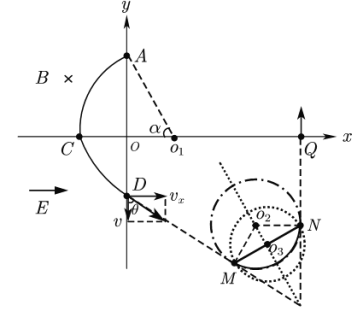
粒子在第二象限做匀速圆周运动，设粒子在第二象限磁场中做匀速圆周运动的半径为r，由牛顿第二定律有

由几何关系有：

可得：r=2d

联立以上各式得：

粒子在第三象限做类平抛运动，设粒子在第三象限电场中运动的时间为t2，y轴方向分运动为匀速直线运动有：

设x轴方向匀加速运动的加速度为a，有：

Eq＝ma

联立各式得：

(2)设粒子在第二象限磁场中运动的时间为t1，AC弧对应的圆心角为α，由几何关系知

可解得：α=60°

由运动学公式有：

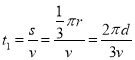
由(1)可知：

所以粒子由A至D过程所用的时间为：

(3)设粒子在D点的速度与y轴负方向夹角为θ，在D处，粒子的x轴分速度：

由合速度与分速度的关系得：

联立可得：θ=60°，故；

设粒子在第四象限磁场中做匀速圆周运动的半径为r1，由牛顿第二定律有

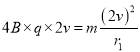
结合(1)得：r1=d；

在第四象限如图，粒子在第四象限运动的轨迹必定与D、Q速度所在直线相切，由于粒子运动轨迹半径为d，故粒子在第四象限运动的轨迹是如图所示的轨迹圆O2，该轨迹圆与速度所在直线相切于M点、与速度所在直线相切于N点，连接MN，由几何关系可知：

MN=

由于M点、N点必须在磁场内，即线段MN在磁场内，故可知磁场面积最小时必定是以MN为直径（如图所示）的圆。即面积最小的磁场半径为：

设磁场的最小面积为S，得

答：（1）第二象限磁感应强度，第三象限电场强度；

（2）粒子由A至D过程所用的时间；

（3）第四象限圆形磁场区域的最小面积。