题目内容
如图，弹簧吊着箱子A，箱内放有物体B，它们的质量均为m， 现对箱子施加竖直向上的力F=4mg，而使系统静止。撤去F的瞬间， A、B的加速度分别为（ ）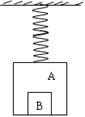
A．aA=aB=g
B．aA="g" ,aB=0
C．aA="2g," aB=g
D．aA="3g," aB=g
D
解析试题分析：解答本题的关键是先研究状态变化前弹簧的弹力，再研究状态变化瞬间的加速度，抓住弹簧的弹力不能突变的特点．撤去F前：设弹簧的弹力大小为f．根据平衡条件得
对整体：
，解得：
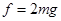
撤去F的瞬间：弹簧的弹力没有来得及变化，大小仍为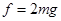
假设A、B之间的弹力突变为零，则根据牛顿第二定律得：
对箱子A：
解得：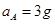
对物体B：
解得：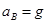
所以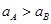
又因物体B处在箱子A的底板之上，因此假设成立．故选D
考点：本题考查了牛顿第二定律、胡克定律及平衡条件等知识点．
练习册系列答案
相关题目
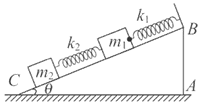
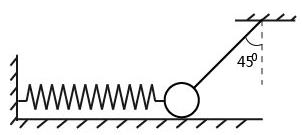
下列四个图中，所有的球都是相同的，且形状规则质量分布均匀．甲球放在光滑斜面和光滑水平面之间，乙球与其右侧的球相互接触并放在光滑的水平面上，丙球与其右侧的球放在另一个大的球壳内部并相互接触，丁球用两根轻质细线吊在天花板上，且其中右侧一根线是沿竖直方向．关于这四个球的受力情况，下列说法正确的是( )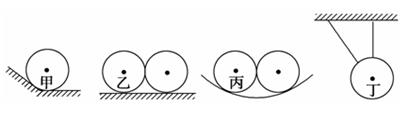
| A．甲球受到两个弹力的作用 |
| B．乙球受到两个弹力的作用 |
| C．丙球受到两个弹力的作用 |
| D．丁球受到两个弹力的作用 |
如图所示，为一轻质弹簧的长度和弹力大小的关系，根据图象判断，正确的结论是( )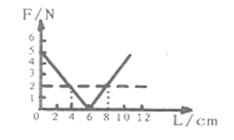
| A．弹簧的劲度系数为lN/m |
| B．弹簧的劲度系数为IOON/m |
| C．弹簧的原长为6cm |
| D．弹簧伸长0.02m时，弹力的大小为4N |
一个弹簧挂30N的重物时，弹簧伸长1.2cm，若改挂100N的重物时，弹簧总长为20cm，则弹簧的原长为（ ）
| A．12cm | B．14cm | C．15cm | D．16cm |
探究弹力和弹簧伸长的关系时，在弹性限度内，悬挂15 N重物时，弹簧长度为0.16 m，悬挂20 N重物时，弹簧长度为0.18 m，则弹簧的原长L0和劲度系数k分别为( )
| A．L0＝0.02 m k＝500 N/m | B．L0＝0.10 m k＝500 N/m |
| C．L0＝0.02 m k＝250 N/m | D．L0＝0.10 m k＝250 N/m |
.当MN中没有电流通过且处于平衡状态时，MN与矩形区域的cd边重合：当MN中有电流通过时，指针示数可表示电流强度．
，
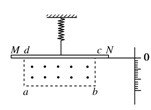
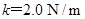，此电流表的量程是多少？(不计通电时电流产生的磁场的作用)