题目内容
14.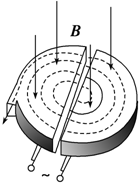 回旋加速器是用来加速带电粒子使它们获得很大动能的仪器,其核心部分是两个D形金属扁盒,两盒分别和一高频交流电源两极相接,以便在盒内的狭缝中形成匀强电场,使粒子每次穿过狭缝时都得到加速(加速时电压为U),两盒放在磁感应强度为B的匀强磁场中,磁场方向垂直于盒底面,粒子源置于盒的圆心附近,若粒子源射出的粒子电荷量为q、质量为m,粒子最大回旋半径为R,求:(设粒子加速时质量不变,且不考虑粒子从粒子源出来时具有的能量)
回旋加速器是用来加速带电粒子使它们获得很大动能的仪器,其核心部分是两个D形金属扁盒,两盒分别和一高频交流电源两极相接,以便在盒内的狭缝中形成匀强电场,使粒子每次穿过狭缝时都得到加速(加速时电压为U),两盒放在磁感应强度为B的匀强磁场中,磁场方向垂直于盒底面,粒子源置于盒的圆心附近,若粒子源射出的粒子电荷量为q、质量为m,粒子最大回旋半径为R,求:(设粒子加速时质量不变,且不考虑粒子从粒子源出来时具有的能量)(1)能加速带电粒子是电场还是磁场,带电粒子在D形盒内做何种运动;
(2)带电粒子离开加速器时的最大速度及最大动能;
(3)带电粒子在D形盒内运动的总时间?
分析 (1)根据粒子在磁场中的受力判断其运动;根据粒子在电场中的运动判断球运动;
(2)由洛伦兹力提供向心力求的半径最大时的速度;
(3)粒子运动的总时间等于粒子在电场和磁场中时间之和.
解答 解:(1)能加速带电粒子的是电场; 带电粒子在盒内做匀速圆周运动.
(2)由qvmB=m$\frac{{v}^{2}}{R}$得
解得vm=$\frac{qBR}{m}$.
最大动能:${E}_{km}=\frac{1}{2}m{v}_{m}^{2}=\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$
(3)由能量守恒得$\frac{1}{2}$mv2=nqU
则离子匀速圆周运动总时间t1=$\frac{nT}{2}$
离子在匀强电场中的加速度为a=$\frac{qU}{md}$
匀加速总时间t2=$\frac{{v}_{m}}{a}$
解得t=t1+t2=$\frac{Bπ{R}^{2}}{2U}+\frac{BRd}{U}$.
答:(1)能加速带电粒子是电场,带电粒子在D形盒内做匀速圆周运动;
(2)带电粒子离开加速器时的最大速度是$\frac{qBR}{m}$,最大动能是$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$;
(3)带电粒子在D形盒内运动的总时间是$\frac{Bπ{R}^{2}}{2U}+\frac{BRd}{U}$.
点评 解决本题的关键知道回旋加速器利用磁场偏转和电场加速实现加速粒子,最大速度决定于D形盒的半径

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
12.检验电荷在电场中受到的电场力为F,测得该点的场强为E;若将检验电荷的电量减小一半,放回原处,则下列说法正确的是( )
| A. | 电场力仍为F,电场强度仍为E | B. | 电场力仍为F,电场强度为$\frac{E}{2}$ | ||
| C. | 电场力为$\frac{F}{2}$,电场强度为$\frac{E}{2}$ | D. | 电场力为$\frac{F}{2}$,电场强度仍为E |
13.从静止开始做匀加速直线运动的物体,前10s内的位移是10m,则该物体运动60s时的位移为( )
| A. | 36m | B. | 60m | C. | 120m | D. | 360m |
9.2015年9月30日7点13分,我国在西昌卫星发射中心用长征三号乙运载火箭成功将1颗新一代北斗导航卫星发射升空,这是我国第4颗新一代北斗导航卫星,也是我国发射的第20颗北斗导航卫星,该卫星是一颗同步卫星.若该卫星质量为m,且已知地球的半径为R,地球表面的重力加速度为g,地球自转的角速度为ω,则该卫星在轨道上运行时所受的万有引力大小为( )
| A. | mω2R | B. | m$\root{3}{g{R}^{2}{ω}^{2}}$ | C. | m$\root{3}{g{R}^{2}{ω}^{4}}$ | D. | 无法求出 |
6.滑块a、b沿水平面上同一条直线发生碰撞;碰撞后两者粘在一起运动;经过一段时间后,从光滑路段进入粗糙路段.两者的位置x随时间t变化的图象如图所示.由图象可知( )
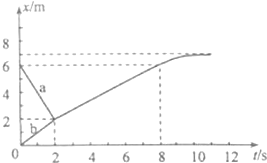

| A. | 相碰前,a在减速,b在加速 | |
| B. | 碰撞后,第1秒内a的速度为$\frac{2}{3}m/s$ | |
| C. | 进入粗糙路段后,a的加速度逐渐减小 | |
| D. | 相碰前,a、b的速度方向相同,加速度方向相反 |
4.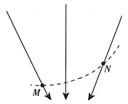 一电场的电场线如图所示,一带电油滴在电场中从N运动到M,运动轨迹如图中虚线所示.若不计空气阻力,则对此带电油滴及其运动的过程,下列说法正确的是( )
一电场的电场线如图所示,一带电油滴在电场中从N运动到M,运动轨迹如图中虚线所示.若不计空气阻力,则对此带电油滴及其运动的过程,下列说法正确的是( )
 一电场的电场线如图所示,一带电油滴在电场中从N运动到M,运动轨迹如图中虚线所示.若不计空气阻力,则对此带电油滴及其运动的过程,下列说法正确的是( )
一电场的电场线如图所示,一带电油滴在电场中从N运动到M,运动轨迹如图中虚线所示.若不计空气阻力,则对此带电油滴及其运动的过程,下列说法正确的是( )| A. | 油滴带正电 | B. | 油滴所受的电场力增大 | ||
| C. | 油滴的电势能增加 | D. | 油滴的动能和电势能之和增加 |
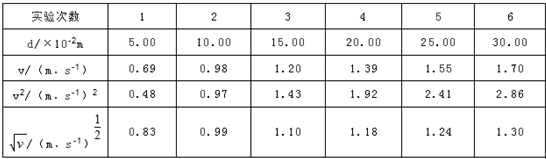
 图中所示的装置可用来探究做功与速度变化的关系.倾角为θ的斜面体固定在实验台上,将光电门固定在斜面体的底端O点,将直径为D的小球从斜面上的不同位置由静止释放.释放点到光电门的距离S依次为5cm、l0cm、15cm、20cm、25cm、30cm.
图中所示的装置可用来探究做功与速度变化的关系.倾角为θ的斜面体固定在实验台上,将光电门固定在斜面体的底端O点,将直径为D的小球从斜面上的不同位置由静止释放.释放点到光电门的距离S依次为5cm、l0cm、15cm、20cm、25cm、30cm.