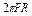题目内容
用铁锤将一铁钉击入木块，设木块对铁钉的阻力与铁钉进入木块内的深度成正比。在铁锤击第一次时，能把铁钉击入木块内1 cm。问击第二次时，能击入多少深度？（设铁锤每次做功相等）
0.41m
考查对功概念的理解能力及理论联系实际抽象建立模型的能力。B级要求。
错解分析：（1）不能据阻力与深度成正比这一特点，将变力求功转化为求平均阻力的功，进行等效替代。（2）不能类比迁移，采用类似据匀变速直线速度-时间图象
求位移的方式，根据F-x图象求功。
解题方法与技巧：解法一：（平均力法）
铁锤每次做功都用来克服铁钉阻力做的功，但摩擦阻力不是恒力，其大小与深度成正比，比例系数为K。
第一次击入深度为x1，平均阻力
=
kx1，做功为W1=x1=kx12。
第二次击入深度为x1到x2，平均阻力
=k（x2+x1），位移为x2-x1，做功为W2=（x2-x1）= k（x22-x12）。
两次做功相等：W1=W2。
解后有：x2=
x1="1.41" cm，
Δx="x2-x1=0.41" cm。
解法二：（图象法）
因为阻力F=kx，以F为纵坐标，F方向上的位移x为横坐标，作出F-x图象（图4-4）。曲线上面积的值等于F对铁钉做的功。
由于两次做功相等，故有：
S1=S2（面积），即：
kx12=k（x2+x1）（x2-x1），
所以Δx="x2-x1=0.41" cm
错解分析：（1）不能据阻力与深度成正比这一特点，将变力求功转化为求平均阻力的功，进行等效替代。（2）不能类比迁移，采用类似据匀变速直线速度-时间图象
求位移的方式，根据F-x图象求功。
解题方法与技巧：解法一：（平均力法）
铁锤每次做功都用来克服铁钉阻力做的功，但摩擦阻力不是恒力，其大小与深度成正比，比例系数为K。
第一次击入深度为x1，平均阻力
=kx1，做功为W1=x1=kx12。第二次击入深度为x1到x2，平均阻力
=k（x2+x1），位移为x2-x1，做功为W2=（x2-x1）= k（x22-x12）。两次做功相等：W1=W2。
解后有：x2=
x1="1.41" cm，Δx="x2-x1=0.41" cm。
解法二：（图象法）
因为阻力F=kx，以F为纵坐标，F方向上的位移x为横坐标，作出F-x图象（图4-4）。曲线上面积的值等于F对铁钉做的功。
由于两次做功相等，故有：
S1=S2（面积），即：
kx12=k（x2+x1）（x2-x1），所以Δx="x2-x1=0.41" cm
练习册系列答案
阅读快车系列答案
相关题目
和R的两个半圆构成.现用大小恒为F的拉力将一光滑小球从A点沿槽道拉至B点，若拉力F的方向时时刻刻均与小球运动方向一致，则此过程中拉力所做的功为（ ）
