题目内容
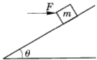（2013?奉贤区二模）一质量为m=2kg的滑块能在倾角为θ=300的足够长的斜面上以a=2.5m/s2匀加速下滑．如图所示，若用一水平推力F作用于滑块，使之由静止开始在t=2s内能沿斜面运动位移s=4m．求：（取g=10m/s2）（1）滑块和斜面之间的动摩擦因数μ；
（2）推力F的大小．
分析：（1）根据牛顿第二定律即可求解；
（2）使滑块沿斜面做匀加速直线运动，有加速度向上和向下两种可能，分别根据牛顿第二定律即可求解．
（2）使滑块沿斜面做匀加速直线运动，有加速度向上和向下两种可能，分别根据牛顿第二定律即可求解．
解答：解：（1）根据牛顿第二定律可得：mgsin30°-μmgcos30°=ma
解得：μ=
（2）使滑块沿斜面做匀加速直线运动，有加速度向上和向下两种可能．
当加速度沿斜面向上时，F cos30°-mgsin30°-μ（F sin30°+mgcos30°）=ma
代入数据得：F=
N
当加速度沿斜面向下时，mgsin30°-F cos30°-μ（F sin30°+mgcos30°）=ma
代入数据得：F=
N
答：（1）滑块和斜面之间的动摩擦因数为
；
（2）推力F的大小为
N或=
N．
解得：μ=
| ||
| 6 |
（2）使滑块沿斜面做匀加速直线运动，有加速度向上和向下两种可能．
当加速度沿斜面向上时，F cos30°-mgsin30°-μ（F sin30°+mgcos30°）=ma
代入数据得：F=
76
| ||
| 5 |
当加速度沿斜面向下时，mgsin30°-F cos30°-μ（F sin30°+mgcos30°）=ma
代入数据得：F=
4
| ||
| 7 |
答：（1）滑块和斜面之间的动摩擦因数为
| ||
| 6 |
（2）推力F的大小为
76
| ||
| 5 |
4
| ||
| 7 |
点评：决本题的关键进行受力分析，运用正交分解，结合牛顿第二定律进行求解，知道合力沿斜面方向，垂直于斜面方向上的合力等于零．
练习册系列答案
相关题目
（2013?奉贤区二模）物体在如图所示的合外力的作用下从静止开始做直线运动．设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2，速度分别是v1和v2，合外力从开始至t0时刻做的功是W1，从t0至2t0时刻做的功是W2，则（ ）
（2013?奉贤区二模）如图所示，小车沿水平地面向右匀加速直线运动，固定在小车上的直杆与水平地面的夹角为θ，杆顶端固定有质量为m的小球．当小车的加速度逐渐增大时，杆对小球的作用力变化的受力图（OO′为沿杆方向）是（ ）
（2013?奉贤区二模）某同学设计了一个电磁冲击钻，其原理示意图如图所示，若发现钻头M突然向右运动，则可能是（ ）
（2013?奉贤区二模）某组同学利用如下器材测定一种电池的电动势和内阻：