题目内容
如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里.一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出.
(1)求电场强度的大小和方向.
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经 时间恰好从半圆形区域的边界射出.求粒子运动加速度的大小.
时间恰好从半圆形区域的边界射出.求粒子运动加速度的大小.
(3)若仅撤去电场,带电粒子仍从O点射入,但速度为原来的4倍,求粒子在磁场中运动的时间.
(1)E=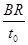 方向沿x轴正方向(2)
方向沿x轴正方向(2)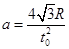 (3)
(3)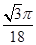 t0
t0
解析试题分析:(1)因为带电粒子进入复合场后做匀速直线运动,则qv0B=qE ①
R=v0t0 ②
由①②联立解得E=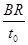 方向沿x轴正方向.
方向沿x轴正方向.
(2)若仅撤去磁场,带电粒子在电场中做类平抛运动,沿y轴正方向做匀速直线运动y=v0· =
=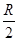 ③
③
沿x轴正方向做匀加速直线运动x=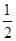 a(
a( )2=
)2=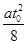 ④
④
由几何关系可知: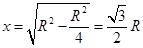 ⑤
⑤
解得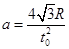
(3)仅有磁场时,入射速度v/=4v0,带电粒子在匀强磁场中做匀速圆周运动,设轨道半径为r,由牛顿定律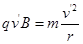 ⑥
⑥
又Eq=ma ⑦
可得 ⑧,
⑧,
由几何知识  ⑨,
⑨,
即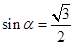 ,
,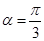 ⑩,
⑩,
带电粒子在磁场中的运动周期 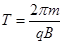 ,则带电粒子在磁场中运动时间t′=
,则带电粒子在磁场中运动时间t′=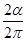 T
T
所以t′=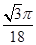 t0
t0
考点:带电粒子在磁场中的运动;类平抛运动。

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
1831年发现电磁感应现象的物理学家是( )
| A.牛顿 | B.伽利略 | C.法拉第 | D.焦耳 |


 小球距N点的距离s为多远。
小球距N点的距离s为多远。 T,粒子的荷质比
T,粒子的荷质比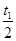 C/kg,不计粒子的重力。问:
C/kg,不计粒子的重力。问:

 的匀强磁场,方向与xoy平面垂直,在x轴上的P(10,0)点,有一放射源,在xoy平面内向各个方向发射速率
的匀强磁场,方向与xoy平面垂直,在x轴上的P(10,0)点,有一放射源,在xoy平面内向各个方向发射速率 的带正电的粒子,粒子的质量为
的带正电的粒子,粒子的质量为 ,电荷量为
,电荷量为 ,求带电粒子能打到y轴上的范围.
,求带电粒子能打到y轴上的范围.

 飞进圆1内部磁场。问:
飞进圆1内部磁场。问: