Question

【题目】如图所示，在竖直平面的xOy坐标系中，Oy竖直向上，Ox水平。设平面内存在沿x轴正方向的恒定风力。一小球从坐标原点沿Oy方向竖直向上抛出，初速度为v0＝4 m/s，不计空气阻力，到达最高点的位置如图中M点所示(坐标格为正方形，g取10 m/s2) 则

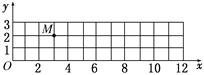
（1）小球在M点的速度大小v1=_________m/s；

（2）在图中定性画出小球的运动轨迹并标出小球落回x轴时的位置N_________；

（3）小球到达N点的速度的大小v2=_________m/s。

Answer 1

【答案】 (1)6 m/s (2)见图；

　(3)4m/s

【解析】试题分析：（1）设正方形的边长为s0。

竖直方向做竖直上抛运动，v0＝gt1；

水平方向做匀加速直线运动，

解得v1＝6 m/s。

（2）由竖直方向的对称性可知，小球再经过t1到x轴，水平方向做初速度为零的匀加速直线运动，所以回到x轴时落到x＝12处，位置N的坐标为（12,0）。

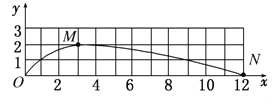
（3）到N点时竖直分速度大小为v0＝4 m/s，

水平分速度vx＝a水平tN＝2v1＝12 m/s，

故。