题目内容
8. 回旋加速器D型盒中央为质子源,D型盒间的交变(方波)电压为U=2×104V,静止质子经电场加速后,进入D型盒,其最大轨道半径R=1m,磁感应强度B=0.5T,质子质量m=1.67×10-27kg,电荷量e=1.6×10-19C.求:
回旋加速器D型盒中央为质子源,D型盒间的交变(方波)电压为U=2×104V,静止质子经电场加速后,进入D型盒,其最大轨道半径R=1m,磁感应强度B=0.5T,质子质量m=1.67×10-27kg,电荷量e=1.6×10-19C.求:(1)质子最初进入D型盒的动能多大?
(2)质子经回旋加速器最后得到的动能多大?
(3)交变电源的频率.
分析 (1)根据质子在电场力作用下,被加速,由动能定理,即可求解;
(2)根据运动半径等于R,结合牛顿第二定律与向心力,即可求解;
(3)根据洛伦兹力提供向心力,即可求出运动的周期,从而确定交流电源的周期.
解答 解:(1)质子在电场中被加速,根据动能定理,
则有最初进入下方D型盒的动能:Ek=eU=1.6×10-19C×2×104V=3.2×10-15J;
(2)根据qvB=m$\frac{{v}^{2}}{R}$ 得,粒子出D形盒时的速度vm=$\frac{qBR}{m}$,
则粒子出D形盒时的动能Ekm=$\frac{1}{2}$m${v}_{m}^{2}$=$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$=$\frac{(1.6×1{0}^{-19})^{2}×0.{5}^{2}×{1}^{2}}{2×1.67×1{0}^{-27}}$=1.9×10-12 J;
(3)由洛伦兹力提供向心力,则有:Bqv=m$\frac{{v}^{2}}{r}$;
而T=$\frac{2πr}{v}$,所以粒子在磁场中运行周期为T=$\frac{2πm}{eB}$;
因一直处于加速状态,则磁场中的周期与交流电源的周期相同,
即为:T=$\frac{2πm}{eB}$
那么交变电源的频率f=$\frac{eB}{2πm}$=$\frac{1.6×1{0}^{-19}×0.5}{2×3.14×1.67×1{0}^{-27}}$=7.6×106Hz;
答:
(1)质子最初进入D型盒的动能3.2×10-15J;
(2)质子经回旋加速器最后得到的动能1.9×10-12 J;
(3)交变电源的频率7.6×106Hz.
点评 考查粒子做匀速圆周的周期公式与半径公式的应用,掌握牛顿第二定律,注意交流电源变化周期与粒子在磁场中偏转周期的关系.

| A. | 只有球壳外表面带负电 | |
| B. | 只有球壳内表面带负电 | |
| C. | 球壳的内表面带正电,外表面带负电 | |
| D. | 小球带负电,球壳内外表面都不带电 |
 如图所示,边长为L的正方形ABCD区域内存在磁感应强度方向垂直于纸面向里,大小为B的匀强磁场,一质量为m,带电荷量为-q的粒子从AB边的中点处垂直于磁感应强度方向射入磁场,速度方向与AB边的夹角为30°,若要求该粒子不从AD边射出磁场,则其速度大小应满足( )
如图所示,边长为L的正方形ABCD区域内存在磁感应强度方向垂直于纸面向里,大小为B的匀强磁场,一质量为m,带电荷量为-q的粒子从AB边的中点处垂直于磁感应强度方向射入磁场,速度方向与AB边的夹角为30°,若要求该粒子不从AD边射出磁场,则其速度大小应满足( )| A. | v≤$\frac{2qBL}{m}$ | B. | v≥$\frac{2qBL}{m}$ | C. | v≤$\frac{qBL}{m}$ | D. | v≥$\frac{qBL}{m}$ |
| A. | 物体的重力势能增加Mgh | B. | 细绳拉力对物体做功Mgh | ||
| C. | 水和物体系统的机械能增加Mgh | D. | 水的机械能减小,物体机械能增加 |

| A. | 甲做匀速直线运动,乙做匀变速直线运动 | |
| B. | 两物体两次相遇的时刻分别是在2s末和6s末 | |
| C. | 乙在6s内运动的加速度方向都是正方向 | |
| D. | 2s后,甲、乙两物体的速度方向相反 |
 在用油膜法估测油酸分子的大小的实验中,用到器材有:浓度为0.05%(体积分数)的油酸酒精溶液、最小刻度为0.1mL的量筒、盛有适量清水的45×50cm2浅盘、痱子粉、橡皮头滴管、玻璃板、彩笔、坐标纸.实验步骤如下:
在用油膜法估测油酸分子的大小的实验中,用到器材有:浓度为0.05%(体积分数)的油酸酒精溶液、最小刻度为0.1mL的量筒、盛有适量清水的45×50cm2浅盘、痱子粉、橡皮头滴管、玻璃板、彩笔、坐标纸.实验步骤如下: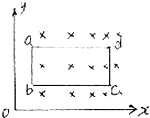 如图所示,矩形线圈边长ab=5cm,ad=10cm,电阻为2Ω.磁场方向垂直线圈平面,磁感应强度沿正x轴均匀增加,且$\frac{△B}{△x}$=10T/m,若使线圈沿正x方向以v=2m/s的速度匀速运动,运动中ab边始终与y轴平行.求运动过程中水平拉力的功率.
如图所示,矩形线圈边长ab=5cm,ad=10cm,电阻为2Ω.磁场方向垂直线圈平面,磁感应强度沿正x轴均匀增加,且$\frac{△B}{△x}$=10T/m,若使线圈沿正x方向以v=2m/s的速度匀速运动,运动中ab边始终与y轴平行.求运动过程中水平拉力的功率.