题目内容
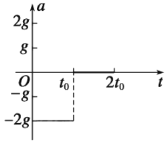
【题目】宇宙间存在一个离其他星体遥远的系统,其中有一种系统如图示,四颗质量均为m的星体位于正方形的顶点,正方形的边长为a,忽略其他星体对它们的引力作用,每颗都在同一平面内绕正方形对角线的交点O做匀速圆周运动,引力常量为G,则

A. 每颗星做圆周运动的线速度大小为![]()
B. 每颗星做圆周运动的角速度大小为![]()
C. 每颗星做圆周运动的周期为2π![]()
D. 每颗星做圆周运动的加速度与质量m有关
【答案】AD
【解析】
星体做匀速圆周运动的轨道半径等于正方形对角线的一半.在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力求出线速度大小,根据角速度、周期、加速度与线速度的关系,即可求出这三个量;
由星体均围绕正方形对角线的交点做匀速圆周运动可知,星体做匀速圆周运动的轨道半径![]()
每颗星体在其他三个星体万有引力的合力作用下围绕正方形对角线的交点做匀速圆周运动,由万有引力定律和向心力公式得:![]()
解得:![]()
角速度为:![]()
周期为: ![]()
加速度:![]() ,故选项AD正确,选项BC错误。
,故选项AD正确,选项BC错误。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目