题目内容
 如图所示,A物体用板托着,位于离地h=1.0m处,轻质细绳通过光滑定滑轮与A、B相连,绳子处于绷直状态,已知A物体质量M=1.5㎏,B物体质量m=1.0kg,现将板抽走,A将拉动B上升,设A与地面碰后不反弹,B上升过程中不会碰到定滑轮,问:B物体在上升过程中离地的最大高度为多大?取g=10m/s2.
如图所示,A物体用板托着,位于离地h=1.0m处,轻质细绳通过光滑定滑轮与A、B相连,绳子处于绷直状态,已知A物体质量M=1.5㎏,B物体质量m=1.0kg,现将板抽走,A将拉动B上升,设A与地面碰后不反弹,B上升过程中不会碰到定滑轮,问:B物体在上升过程中离地的最大高度为多大?取g=10m/s2.分析:A、B组成的系统机械能守恒,系统重力势能的减小量等于系统动能的增加量,根据系统机械能守恒求出A落地前瞬间的速度.A落地后,绳子的拉力为0,B物体只有重力做功,根据机械能守恒得出B还能上升的高度,从而得出B物体上升过程中离地的最大高度.
解答:解:在A下降B上升的过程中,A、B系统机械能守恒,由机械能守恒定律得
Mgh-mgh=
(M+m)v2
v=
=
m/s=2m/s.
A落地后,B物体仅受重力,机械能守恒,设B物体还能上升的高度为h′,有
mv2=mgh′
代入数据得,h′=
=0.2m
H=h′+h=1.2m
答:B物体上升过程中离地的最大高度为1.2m.
Mgh-mgh=
| 1 |
| 2 |
v=
|
|
A落地后,B物体仅受重力,机械能守恒,设B物体还能上升的高度为h′,有
| 1 |
| 2 |
代入数据得,h′=
| ||
| 10 |
H=h′+h=1.2m
答:B物体上升过程中离地的最大高度为1.2m.
点评:解决本题的关键知道A落地前,A、B两物体除重力做功外,还有拉力做功,单个物体机械能不守恒,但对于A、B组成的系统,只有重力做功,系统机械能守恒.A着地后,B物体仅受重力,机械能守恒.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 如图所示,A物体用板托着,位于离地h=1.0m处,轻质细绳通过光滑定滑轮与A、B相连,绳子处于绷直状态,已知A物体质量M=1.5㎏,B物体质量m=1.0kg,现将板抽走,A将拉动B上升,设A与地面碰后不反弹,B上升过程中不会碰到定滑轮,问:
如图所示,A物体用板托着,位于离地h=1.0m处,轻质细绳通过光滑定滑轮与A、B相连,绳子处于绷直状态,已知A物体质量M=1.5㎏,B物体质量m=1.0kg,现将板抽走,A将拉动B上升,设A与地面碰后不反弹,B上升过程中不会碰到定滑轮,问: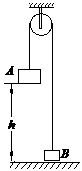 如图所示,A物体用板托着,位于离地h=1.0m处,轻质细绳通过光滑定滑轮与A、B相连,绳子处于绷直状态,已知A物体质量M=1.5㎏,B物体质量m=1.0kg,现将板抽走,A将拉动B上升,设A与地面碰后不反弹,B上升过程中不会碰到定滑轮,问:B物体在上升过程中离地的最大高度为多大?取g =10m/s2.
如图所示,A物体用板托着,位于离地h=1.0m处,轻质细绳通过光滑定滑轮与A、B相连,绳子处于绷直状态,已知A物体质量M=1.5㎏,B物体质量m=1.0kg,现将板抽走,A将拉动B上升,设A与地面碰后不反弹,B上升过程中不会碰到定滑轮,问:B物体在上升过程中离地的最大高度为多大?取g =10m/s2.