题目内容
（2012?上海）如图，将质量m=0.1kg的圆环套在固定的水平直杆上．环的直径略大于杆的截面直径．环与杆间动摩擦因数μ=0.8．对环施加一位于竖直平面内斜向上，与杆夹角θ=53°的拉力F，使圆环以a=4.4m/s2的加速度沿杆运动，求F的大小．（取sin53°=0.8，cos53°=0.6，g=10m/s2）．分析：对环受力分析，受重力、拉力、弹力和摩擦力，其中弹力可能向上，也可能向下；要分两种情况根据牛顿第二定律列方程求解即可．
解答：解：对环受力分析，受重力、拉力、弹力和摩擦力；令Fsin53°=mg，F=1.25N 此时无摩擦力．
当F＜1.25N 时，杆对环的弹力向上，由牛顿定律Fcosθ-μFN=ma，FN+Fsinθ=mg，解得F=1N
当F＞1.25N时，杆对环的弹力向下，由牛顿定律Fcosθ-μFN=ma，Fsinθ=mg+FN，解得F=9N
答：F的大小为1N或者9N．
当F＜1.25N 时，杆对环的弹力向上，由牛顿定律Fcosθ-μFN=ma，FN+Fsinθ=mg，解得F=1N
当F＞1.25N时，杆对环的弹力向下，由牛顿定律Fcosθ-μFN=ma，Fsinθ=mg+FN，解得F=9N
答：F的大小为1N或者9N．
点评：本题要分两种情况对物体受力分析，然后根据平衡条件列方程求解，关键是分情况讨论．
练习册系列答案
阅读快车系列答案
相关题目
（2012?上海）如图，光滑斜面固定于水平面，滑块A、B叠放后一起冲上斜面，且始终保持相对静止，A上表面水平．则在斜面上运动时，B受力的示意图为（ ）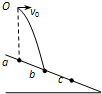
（2012?上海）如图所示，斜面上a、b、c三点等距，小球从a点正上方O点抛出，做初速为v0的平抛运动，恰落在b点．若小球初速变为v，其落点位于c，则（ ）
（2012?上海）如图，竖直轻质悬线上端固定，下端与均质硬棒AB中点连接，棒长为线长的二倍．棒的A端用铰链墙上，棒处于水平状态．改变悬线的长度，使线与棒的连接点逐渐右移，并保持棒仍处于水平状态．则悬线拉力（ ）