题目内容
（2012?上海）如图，可视为质点的小球A、B用不可伸长的细软轻线连接，跨过固定在地面上半径为R有光滑圆柱，A的质量为B的两倍．当B位于地面时，A恰与圆柱轴心等高．将A由静止释放，B上升的最大高度是
（ ）
（ ）
分析：开始AB一起运动，A落地后，B做竖直上抛运动，B到达最高点时速度为零；由动能定理可以求出B上升的最大高度．
解答：解：设B的质量为m，则A的质量为2m，
以A、B组成的系统为研究对象，
在A落地前，由动能定理可得：
-mgR+2mgR=
（m+2m）v2-0，
以B为研究对象，在B上升过程中，
由动能定理可得：-mgh=0-
mv2，
则B上升的最大高度H=R+h，
解得：H=
；
故选C．
以A、B组成的系统为研究对象，
在A落地前，由动能定理可得：
-mgR+2mgR=
| 1 |
| 2 |
以B为研究对象，在B上升过程中，
由动能定理可得：-mgh=0-
| 1 |
| 2 |
则B上升的最大高度H=R+h，
解得：H=
| 4R |
| 3 |
故选C．
点评：B的运动分两个阶段，应用动能定理即可求出B能上升的最大高度．
练习册系列答案
相关题目
（2012?上海）如图，光滑斜面固定于水平面，滑块A、B叠放后一起冲上斜面，且始终保持相对静止，A上表面水平．则在斜面上运动时，B受力的示意图为（ ）
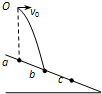（2012?上海）如图所示，斜面上a、b、c三点等距，小球从a点正上方O点抛出，做初速为v0的平抛运动，恰落在b点．若小球初速变为v，其落点位于c，则（ ）
（2012?上海）如图，将质量m=0.1kg的圆环套在固定的水平直杆上．环的直径略大于杆的截面直径．环与杆间动摩擦因数μ=0.8．对环施加一位于竖直平面内斜向上，与杆夹角θ=53°的拉力F，使圆环以a=4.4m/s2的加速度沿杆运动，求F的大小．（取sin53°=0.8，cos53°=0.6，g=10m/s2）．
（2012?上海）如图，竖直轻质悬线上端固定，下端与均质硬棒AB中点连接，棒长为线长的二倍．棒的A端用铰链墙上，棒处于水平状态．改变悬线的长度，使线与棒的连接点逐渐右移，并保持棒仍处于水平状态．则悬线拉力（ ）