��Ŀ����
����Ŀ����ͼ��ʾ��һ�⻬ˮƽ����������Ϊm�Ĺ⻬������A��A�Ҷ���ˮƽ��ƽ�����ӣ�һ����Ϊm��С��C����������A��б���ϣ���ˮƽ��ĸ߶�Ϊh��С��C�Ӿ�ֹ��ʼ���£�Ȼ��������Ϊ2m��B������������![]() ��ײʱ�伫�̣�����е����ʧ
��ײʱ�伫�̣�����е����ʧ![]() ��
��
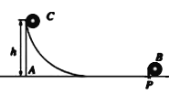
��1��С��C��������A����ʱ��A��C�ٶȴ�С��
��2��С��C��С��B������ײ��С��C�ܷ���������A����Ҫ��д������������̣�ֻ�ж��ܷ��ϲ��÷���
���𰸡���1��![]() ��2�����ܡ�
��2�����ܡ�
��������
��1����ײ����ϵͳ�����غ㣬Ӧ�ö����غ㶨�����е���غ㶨��������ʣ�
��2��Ӧ�ö����غ㶨�����е���غ㶨�ɿ������C�����ʣ��Ӷ��ж��ܷ���A��
��2����С��C����A����ʱ�ٶȴ�СΪv0����ʱ��A�ٶȴ�СΪvA��С��C�˶�����A��͵�Ĺ����У�ѡ������Ϊ��������ˮƽ�����ɶ����غ㶨�ɵã�mv0-mvA=0��
�ɻ�е���غ㶨�ɵã�mgh��![]() mv02+
mv02+![]() mvA2��
mvA2��
��ã�vA��v0��![]() ��
��
��С��C��B�����������ٶȷֱ�ΪvC��vB��ѡ������Ϊ������
����С��C�����B������ȫ�����������ɶ����غ㶨�ɵã�mv0=mvC+2mvB��
�ɻ�е���غ㶨�ɵã�![]() mv02��
mv02��![]() mvC2+
mvC2+![]() mvB2��
mvB2��
��ã�vB��![]() ��vC��
��vC��![]() ��
��
��vC<vA����С��C��С��B������ײ��С��C������������A��