题目内容
如图所示,内壁光滑半径为R的圆形轨道,固定在竖直平面内.质量为m1的小球静止在轨道最低点,另一质量为m2的小球(两小球均可视为质点)从内壁上与圆心O等高的位置由静止释放,运动到最低点时与m1发生碰撞并粘在一起.求
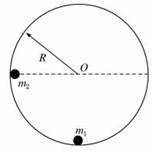
⑴小球m2刚要与m1发生碰撞时的速度大小;
⑵碰撞后,m1?m2能沿内壁运动所能达到的最大高度(相对碰撞点).

⑴小球m2刚要与m1发生碰撞时的速度大小;
⑵碰撞后,m1?m2能沿内壁运动所能达到的最大高度(相对碰撞点).
(1)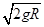 ;(2)
;(2)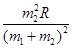
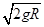 ;(2)
;(2)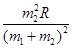
试题分析:(1)设小球m2刚要与m1发生碰撞时的速度大小为v0,由机械能守恒定律可得:
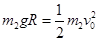 ①
① 解得:
 ②
②(2)设两球碰撞后,m1m2两球粘在一起的速度为v,由动量守恒定律可得:
m2vo=(m1+m2)v ③
两球碰撞后上升的最大高度为h,由机械能守恒定律可得:
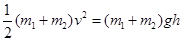 ④
④由②③④可得:


练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目

 )处自由下落,与斜面做无能量损失的碰撞后水平抛出.小球自由下落的落点距斜面左侧的水平距离x满足一定条件时,小球能直接落到水平地面上.
)处自由下落,与斜面做无能量损失的碰撞后水平抛出.小球自由下落的落点距斜面左侧的水平距离x满足一定条件时,小球能直接落到水平地面上.
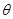 角(
角(

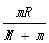
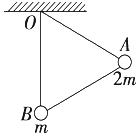
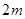 的小球,B处固定质量为
的小球,B处固定质量为 的小球,支架悬挂在O点,可绕过O点并与支架所在平面相垂直的固定轴转动.开始时OB与地面相垂直.放手后开始运动,在不计任何阻力的情况下,下列说法不正确的是( )
的小球,支架悬挂在O点,可绕过O点并与支架所在平面相垂直的固定轴转动.开始时OB与地面相垂直.放手后开始运动,在不计任何阻力的情况下,下列说法不正确的是( )