题目内容
10.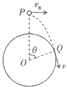 如图所示,半径为R的圆环固定在竖直面内,小球在圆心O正上方的P点以初速度v0水平抛出,运动轨迹恰与圆环相切于Q点,若OQ与OP间的夹角为θ,不计空气阻力,重力加速度为g,则( )
如图所示,半径为R的圆环固定在竖直面内,小球在圆心O正上方的P点以初速度v0水平抛出,运动轨迹恰与圆环相切于Q点,若OQ与OP间的夹角为θ,不计空气阻力,重力加速度为g,则( )| A. | 从P点运动到Q点的时间为$\frac{R}{{v}_{0}sinθ}$ | B. | 从P点运动到Q点的时间为$\frac{Rcosθ}{{v}_{0}}$ | ||
| C. | 小球运动到Q点时的速度为$\frac{{v}_{0}}{sinθ}$ | D. | 小球运动到Q点时的速度为$\frac{{v}_{0}}{cosθ}$ |
分析 小球做平抛运动,根据圆的几何知识可以求得小球在水平方向的位移的大小,根据水平方向的匀速直线运动可以求得时间的大小.根据平行四边形定则求出Q点的速度.
解答 解:AB、过Q点做OP的垂线,根据几何关系可知,小球在水平方向上的位移的大小为Rsinθ,
根据Rsinθ=v0t,
可得时间为:t=$\frac{Rsinθ}{{v}_{0}}$,故A错误,B错误.
CD、根据几何关系知,Q点的速度方向与水平方向的夹角为θ,根据平行四边形定则知,小球运动到Q点时的速度为vQ=$\frac{{v}_{0}}{cosθ}$,故C错误,D正确.
故选:D.
点评 本题对平抛运动规律的直接的应用,知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.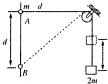 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点正下方距离为d处,现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点正下方距离为d处,现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点正下方距离为d处,现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点正下方距离为d处,现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )| A. | 环到达B处时,环与重物的速度大小相等 | |
| B. | 环从A到B,细绳对重物做功等于重物增加的动能 | |
| C. | 环能下降的最大高度为$\frac{4}{3}$d | |
| D. | 环到达B处时,重物上升的高度h=$\frac{d}{2}$ |
18.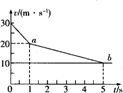 雾霾天气对公路、铁路、航空、航运等均产生重要影响,雾、霾会造成空气质量下降,影响生态环境,给人体健康带来较大危害,在我国治理雾霾已刻不容缓,在一大雾天,一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方30m处有一辆大卡车以10m/s的速度同方向匀速行驶,小汽车紧急刹车,刹车过程中刹车失灵,如图所示,a、b分别为小汽车和大卡车的v-t图象,以下说法正确的是( )
雾霾天气对公路、铁路、航空、航运等均产生重要影响,雾、霾会造成空气质量下降,影响生态环境,给人体健康带来较大危害,在我国治理雾霾已刻不容缓,在一大雾天,一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方30m处有一辆大卡车以10m/s的速度同方向匀速行驶,小汽车紧急刹车,刹车过程中刹车失灵,如图所示,a、b分别为小汽车和大卡车的v-t图象,以下说法正确的是( )
 雾霾天气对公路、铁路、航空、航运等均产生重要影响,雾、霾会造成空气质量下降,影响生态环境,给人体健康带来较大危害,在我国治理雾霾已刻不容缓,在一大雾天,一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方30m处有一辆大卡车以10m/s的速度同方向匀速行驶,小汽车紧急刹车,刹车过程中刹车失灵,如图所示,a、b分别为小汽车和大卡车的v-t图象,以下说法正确的是( )
雾霾天气对公路、铁路、航空、航运等均产生重要影响,雾、霾会造成空气质量下降,影响生态环境,给人体健康带来较大危害,在我国治理雾霾已刻不容缓,在一大雾天,一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方30m处有一辆大卡车以10m/s的速度同方向匀速行驶,小汽车紧急刹车,刹车过程中刹车失灵,如图所示,a、b分别为小汽车和大卡车的v-t图象,以下说法正确的是( )| A. | 因刹车失灵前小汽车已减速,不会追尾 | |
| B. | 在t=5s时追尾 | |
| C. | 在t=3s时追尾 | |
| D. | 若刹车不失灵不会追尾 |
5.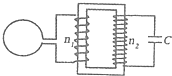 如图所示,左侧的圆形导电环半径为r=2.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容为C=100pF的电容器相连,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁场磁感应强度B的变化率$\frac{△B}{△t}$=100$\sqrt{2}$πsinωt(T/s),若电容器带电量的最大值为1.41×10-9C,则所用理想变压器的原副线圈的匝数之比是(取π2=10)( )
如图所示,左侧的圆形导电环半径为r=2.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容为C=100pF的电容器相连,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁场磁感应强度B的变化率$\frac{△B}{△t}$=100$\sqrt{2}$πsinωt(T/s),若电容器带电量的最大值为1.41×10-9C,则所用理想变压器的原副线圈的匝数之比是(取π2=10)( )
 如图所示,左侧的圆形导电环半径为r=2.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容为C=100pF的电容器相连,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁场磁感应强度B的变化率$\frac{△B}{△t}$=100$\sqrt{2}$πsinωt(T/s),若电容器带电量的最大值为1.41×10-9C,则所用理想变压器的原副线圈的匝数之比是(取π2=10)( )
如图所示,左侧的圆形导电环半径为r=2.0cm,导电环与一个理想变压器的原线圈相连,变压器的副线圈两端与一个电容为C=100pF的电容器相连,导电环的电阻不计,环中有垂直于圆环平面的变化磁场,磁场磁感应强度B的变化率$\frac{△B}{△t}$=100$\sqrt{2}$πsinωt(T/s),若电容器带电量的最大值为1.41×10-9C,则所用理想变压器的原副线圈的匝数之比是(取π2=10)( )| A. | 25:1 | B. | 1:25 | C. | 141:4 | D. | 4:141 |
15.关于热学知识,下列叙述中正确的是( )
| A. | 布朗运动就是液体分子或者气体分子的热运动 | |
| B. | 温度降低,物体内所有分子运动的速率不一定都变小 | |
| C. | 气体分子间距离减小时,分子间斥力增大,引力减小 | |
| D. | 大颗粒的粗盐磨成细盐,仍然是晶体 | |
| E. | 第二类永动机不违背能量守恒定律,但无法制造出来 |
16.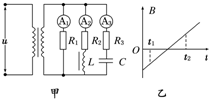 图甲所示电路中,A1、A2、A3为相同的电流表,C为电容器,电阻R1、R2、R3的阻值相同,线圈L的电阻不计.在某段时间内理想变压器原线圈内磁场的变化如图乙所示,则在t1~t2时间内( )
图甲所示电路中,A1、A2、A3为相同的电流表,C为电容器,电阻R1、R2、R3的阻值相同,线圈L的电阻不计.在某段时间内理想变压器原线圈内磁场的变化如图乙所示,则在t1~t2时间内( )
 图甲所示电路中,A1、A2、A3为相同的电流表,C为电容器,电阻R1、R2、R3的阻值相同,线圈L的电阻不计.在某段时间内理想变压器原线圈内磁场的变化如图乙所示,则在t1~t2时间内( )
图甲所示电路中,A1、A2、A3为相同的电流表,C为电容器,电阻R1、R2、R3的阻值相同,线圈L的电阻不计.在某段时间内理想变压器原线圈内磁场的变化如图乙所示,则在t1~t2时间内( )| A. | 电流表A1的示数比A2的小 | B. | 电流表A1和A2的示数相同 | ||
| C. | 电流表A2的示数比A3的小 | D. | 电流表的示数都不为零 |
17.一列沿x轴传播的简谐横波在某时刻的波形图如图所示,波速为20m/s,则下列说法中正确的是( )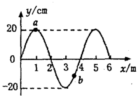

| A. | 从图示时刻开始,质点b的加速度一定增大 | |
| B. | 图示时刻,质点a的加速度方向一定沿y轴负方向 | |
| C. | 若此波遇到另一列波并发生稳定干涉现象,则另一列波的频率为50Hz | |
| D. | 从图示时刻开始,经过0.1s,质点a沿波传播方向迁移了40 cm |