Question

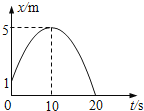
【题目】如图所示，OO′为竖直转轴，MN为固定在OO′上的水平光滑杆，有两个质量相同的金属球A、B套在水平杆上，AC、BC两根抗拉能力相同的细绳一端连接金属球，另一端C固定在转轴OO′上，当两绳拉直时，A、B两球转动的半径之比恒为2∶1.若转轴角速度逐渐增大，则(　　)

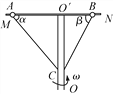
A. AC绳先断 B. BC绳先断 C. 两绳同时断 D. 不能确定哪根绳先断

Answer 1

【答案】A

【解析】试题分析：设绳子与水平方向的夹角为，绳子拉力的分力来提供向心力，根据牛顿第二定律得出：，其中为做圆周运动的轨道半径，（L为绳子长度），推导出拉力可以看出拉力与绳子与水平方向的夹角无关，两小球是同轴转动，角速度相等，质量也相等，拉力只与绳子的长度有关，由图可知绳子AC的长度大于BC绳子，当角速度增大时，AC绳先达到最大拉力，所以AC绳子先断，A项正确；B、C、D项错误。