题目内容
【题目】一弹簧秤秤盘的质量 M=1.5kg,盘内放一个质量 m=10.5kg 的物体 P,弹簧 质量忽略不计,轻弹簧的劲度系数 k=800N/m,系统原来处于静止状态,如图 所示。现给物体 P 施加一竖直向上的拉力 F,使 P 由静止开始 向上作匀加速直线运动。已知在前 0.2s 时间内 F 是变力,在 0.2s 以后是 恒力。取 g=10m/s2。
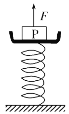
(1)未施加力 F 时,弹簧的压缩量.
(2)物体做匀加速直线运动的加速度大小.
【答案】(1)0.15m;(2)6m/s2
【解析】
(1)未施加力F时,对P和盘整体为研究对象,由平衡条件和胡克定律得出弹簧的压缩量.
(2)在前0.2s时间内F是变力,在0.2s以后是恒力,说明在0.2s时刻物体P与秤盘开始分离,此时它们之间的弹力恰好为零,根据牛顿第二定律此时盘的加速度与弹簧压缩量的关系式.整体过程中盘的位移等于弹簧压缩量之差,求出盘的位移,由位移公式得出位移与加速度的关系式,再联立求出加速度.
(1)设P的质量为m,盘的质量为M.未施加力F时,以物体P和盘整体为研究对象,由平衡条件和胡克定律得:(m+M)g=kx0
解得弹簧的压缩量为:x0=0.15m
(2)刚起动时F有最小值(设为F1),对P、M整体,应用牛顿第二定律得
F1+kx0-(m+M)g=(m+M)a ②
比较①②式,即有 F1=(m+M)a ③
当t=0.2s后P离开了M,0.2s时P、M间挤压力恰为零,F有最大值(设为F2),对P由牛顿第二定律得F2-mg=ma④
此时弹簧压缩量设为x,对M有kx-Mg=Ma⑤
对P、M运动情况,由运动学知识得x0-x=![]() at2 ⑥
at2 ⑥
⑤⑥式联立解得a=6m/s2

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目