题目内容
14.总质量为M的火车在平直轨道上以速度V匀速行驶,尾部有一节质量为m的车厢突然脱钩,设机车的牵引线恒定不变,阻力与质量成正比,则脱钩车厢停下来时,列车前端的速度多大?思考:若车在行进中所受阻力为车重的k倍,当脱钩车厢停下时,距列车的距离有多远?分析 将整节列车作为整体分析,则整体受力平衡,由动量守恒定律可求得前车的速度.
根据牛顿第二定律分别研究脱钩车厢和前部列车,再运用运动学公式求解距离.
解答 解:因整车匀速运动,故整体合外力为零; 由动量守恒,选列车的速度方向为正方向,可得:
Mv=(M-m)v′
解得前面列车的速度为:v′=$\frac{Mv}{M-m}$
若车在行进中所受阻力为车重的k倍,当脱钩车厢停下时,
根据牛顿第二定律得脱钩车厢加速度a=kg,
所以当脱钩车厢停下时的时间t=$\frac{v}{kg}$,
脱钩车厢前进的距离是x1=$\frac{{v}^{2}}{2kg}$,
前部列车的加速度a′=$\frac{kmg}{M-m}$,
前部列车的前进的距离是x2=$\frac{v+v′}{2}$×t=$\frac{2Mv-mv}{2(M-m)}$×$\frac{v}{kg}$
所以当脱钩车厢停下时,距列车的距离是△x=$\frac{(2M-m{)v}^{2}}{2(M-m)kg}$-$\frac{{v}^{2}}{2kg}$
答:脱钩车厢停下来时,列车前端的速度是$\frac{Mv}{M-m}$,当脱钩车厢停下时,距列车的距离是$\frac{(2M-m{)v}^{2}}{2(M-m)kg}$-$\frac{{v}^{2}}{2kg}$.
点评 本题是脱钩问题,抓住整体的合外力为零,动量守恒是解题的关键,掌握牛顿第二定律和运动学公式的应用.

练习册系列答案
相关题目
4. 如图所示,光滑的水平桌面上放着两个完全相同的环形金属圈,原来均静止、且彼此绝缘.当一条形磁铁的N极由上向它们运动时,a、b两线圈将( )
如图所示,光滑的水平桌面上放着两个完全相同的环形金属圈,原来均静止、且彼此绝缘.当一条形磁铁的N极由上向它们运动时,a、b两线圈将( )
 如图所示,光滑的水平桌面上放着两个完全相同的环形金属圈,原来均静止、且彼此绝缘.当一条形磁铁的N极由上向它们运动时,a、b两线圈将( )
如图所示,光滑的水平桌面上放着两个完全相同的环形金属圈,原来均静止、且彼此绝缘.当一条形磁铁的N极由上向它们运动时,a、b两线圈将( )| A. | 均静止不动 | B. | 彼此靠近 | C. | 相互远离 | D. | 都向上跳起 |
5.发现万有引力定律的物理学家是( )
| A. | 开普勒 | B. | 牛顿 | C. | 爱因斯坦 | D. | 麦克斯韦 |
9. 如图所示,等腰直角三角形ABC中存在匀强磁场,比荷相同的两个粒子沿AB方向射入磁场,分别从AC边上的D(AC的中点),C两孔射出,则( )
如图所示,等腰直角三角形ABC中存在匀强磁场,比荷相同的两个粒子沿AB方向射入磁场,分别从AC边上的D(AC的中点),C两孔射出,则( )
 如图所示,等腰直角三角形ABC中存在匀强磁场,比荷相同的两个粒子沿AB方向射入磁场,分别从AC边上的D(AC的中点),C两孔射出,则( )
如图所示,等腰直角三角形ABC中存在匀强磁场,比荷相同的两个粒子沿AB方向射入磁场,分别从AC边上的D(AC的中点),C两孔射出,则( )| A. | 从C,D两孔射出的粒子的运动半径大小之比为RC:RD=2:1 | |
| B. | 从C,D两孔射出的粒子的出射速度大小之比为WC:WD=1:1 | |
| C. | 从C,D两孔射出的粒子在磁场中运动周期之比为TC:TD=2:1 | |
| D. | 从C,D两孔射出的粒子在磁场中的运动时间之比为tC:tD=1:1 |
19. 如图被誉为“豪小子”的华裔球员林书豪在NBA赛场上投二分球时的照片.假设林书豪准备投篮前先曲腿下蹲,再竖直向上跃起.已知林书豪的质量为m,双脚离开地面时的速度为v,从开始下蹲到跃起过程中重心上升的高度为h,重力加速度为g,则( )
如图被誉为“豪小子”的华裔球员林书豪在NBA赛场上投二分球时的照片.假设林书豪准备投篮前先曲腿下蹲,再竖直向上跃起.已知林书豪的质量为m,双脚离开地面时的速度为v,从开始下蹲到跃起过程中重心上升的高度为h,重力加速度为g,则( )
 如图被誉为“豪小子”的华裔球员林书豪在NBA赛场上投二分球时的照片.假设林书豪准备投篮前先曲腿下蹲,再竖直向上跃起.已知林书豪的质量为m,双脚离开地面时的速度为v,从开始下蹲到跃起过程中重心上升的高度为h,重力加速度为g,则( )
如图被誉为“豪小子”的华裔球员林书豪在NBA赛场上投二分球时的照片.假设林书豪准备投篮前先曲腿下蹲,再竖直向上跃起.已知林书豪的质量为m,双脚离开地面时的速度为v,从开始下蹲到跃起过程中重心上升的高度为h,重力加速度为g,则( )| A. | 从地面跃起过程中,地面对他所做的功为零 | |
| B. | 从地面跃起过程中,地面对他所做的功为$\frac{1}{2}$mv2+mgh | |
| C. | 从下蹲到离开地面上升过程中,他的机械能守恒 | |
| D. | 从离开地面到再次落回地面的过程中,他一直处于失重状态 |
4.某楼梯口的电灯开关装有传感器,天黑时出现声音才能发光,白天即使有声音,电灯也不能发光,该开关中有两种传感器,它们可能是( )
| A. | 光敏电阻 | B. | 热敏电阻 | C. | 霍尔元件 | D. | 声音传感器 |
 飞机若仅依靠自身喷气式发动机推力起飞需要较长的跑道,某同学设计在航空母舰上安装电磁弹射器以缩短飞机起飞距离,他的设计思想如下:如图所示,航空母舰的水平跑道总长l=180m,其中电磁弹射器是一种长度为l1=120m的直线电机,这种直线电机从头至尾可以提供一个恒定的牵引力F牵.一架质量为m=2.0×104kg的飞机,其喷气式发动机可以提供恒定的推力F推=1.2×105N.考虑到飞机在起飞过程中受到的阻力与速度大小有关,假设在电磁弹射阶段的平均阻力为飞机重力的0.05倍,在后一阶段的平均阻力为飞机重力的0.2倍.
飞机若仅依靠自身喷气式发动机推力起飞需要较长的跑道,某同学设计在航空母舰上安装电磁弹射器以缩短飞机起飞距离,他的设计思想如下:如图所示,航空母舰的水平跑道总长l=180m,其中电磁弹射器是一种长度为l1=120m的直线电机,这种直线电机从头至尾可以提供一个恒定的牵引力F牵.一架质量为m=2.0×104kg的飞机,其喷气式发动机可以提供恒定的推力F推=1.2×105N.考虑到飞机在起飞过程中受到的阻力与速度大小有关,假设在电磁弹射阶段的平均阻力为飞机重力的0.05倍,在后一阶段的平均阻力为飞机重力的0.2倍. 在科学研究中,可以通过在适当的区域施加磁场控制带电粒子的运动.竖直平行正对放置的两金属板A、K间有电压为U的加速电场,S1、S2为A、K板上的两个小孔,且S1和S2在同一水平直线上,如图所示.质量为m、电荷量为q的粒子,从粒子源N右方的小孔S1不断飘入加速电场,其初速度可视为零,然后经过小孔S2垂直于磁场方向进入匀强磁场控制区,粒子经磁场偏转后离开磁场并打在水平放置的感光胶片上,离开磁场时粒子束的等效电流为I,不考虑粒子重力及粒子间的相互作用.
在科学研究中,可以通过在适当的区域施加磁场控制带电粒子的运动.竖直平行正对放置的两金属板A、K间有电压为U的加速电场,S1、S2为A、K板上的两个小孔,且S1和S2在同一水平直线上,如图所示.质量为m、电荷量为q的粒子,从粒子源N右方的小孔S1不断飘入加速电场,其初速度可视为零,然后经过小孔S2垂直于磁场方向进入匀强磁场控制区,粒子经磁场偏转后离开磁场并打在水平放置的感光胶片上,离开磁场时粒子束的等效电流为I,不考虑粒子重力及粒子间的相互作用.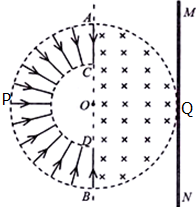 “太空粒子探测器”由加速、偏转和收集三部分装置组成,其原理如图所示:辐射状的加速电场区域边界为两个同心半圆弧$\widehat{AB}$和$\widehat{CD}$,圆心为O,弧$\widehat{AB}$的半径为L,P为弧$\widehat{AB}$的中点,两圆弧间的电势差大小为U.足够长的收集板MN平行边界ACDB,O到MN板的距离OQ为L.在边界ACDB和收集板MN之间有一以O为圆心,L为半径的半圆形匀强磁场,磁场方向垂直纸面向内.假设太空中漂浮着质量为m,电量为q的带正电粒子,它们能均匀地吸附到弧$\widehat{APB}$上,并被加速电场从静止开始加速,不计粒子间的相互作用和其它星球对粒子引力的影响.
“太空粒子探测器”由加速、偏转和收集三部分装置组成,其原理如图所示:辐射状的加速电场区域边界为两个同心半圆弧$\widehat{AB}$和$\widehat{CD}$,圆心为O,弧$\widehat{AB}$的半径为L,P为弧$\widehat{AB}$的中点,两圆弧间的电势差大小为U.足够长的收集板MN平行边界ACDB,O到MN板的距离OQ为L.在边界ACDB和收集板MN之间有一以O为圆心,L为半径的半圆形匀强磁场,磁场方向垂直纸面向内.假设太空中漂浮着质量为m,电量为q的带正电粒子,它们能均匀地吸附到弧$\widehat{APB}$上,并被加速电场从静止开始加速,不计粒子间的相互作用和其它星球对粒子引力的影响.