题目内容
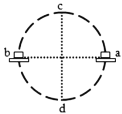
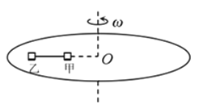
【题目】如图所示，用长为L的轻绳（轻绳不可伸长）连接的甲、乙两物块（均可视为质点），放置在水平圆盘上，甲、乙连线的延长线过圆盘的圆心O，甲与圆心O的距离也为L，甲、乙两物体的质量均为m，与圆盘间的动摩擦因数均为μ，物块与圆盘间的最大静摩擦力等于滑动摩擦力，甲、乙始终相对圆盘静止，则下列说法中正确的是（ ）
A. 圆盘转动的角速度最大为
B. 圆盘转动的角速度最大为
C. 轻绳最大弹力为
D. 轻绳最大弹力
【答案】BC
【解析】
当ω较小时，甲乙均由静摩擦力充当向心力，ω增大，由F=mω2r可知，它受到的静摩擦力也增大，而r甲=L，r乙=2L，r甲<r乙，所以乙受到的静摩擦力先达到最大，此后ω继续增大，要保证乙不滑动，轻绳产生弹力并增大，甲受到的静摩擦力继续增大，直到甲受到的静摩擦力也达到最大，此时ω最大，轻绳弹力T也最大；对甲乙整体：
，解得
对甲：
，解得
；故圆盘转动的角速度最大为 
，轻绳弹力最大为
，故选BC.
练习册系列答案
相关题目
