题目内容
如图所示，水平轨道与竖直平面内的圆弧轨道平滑连接后固定在水平地面上，圆弧轨道B端的切线沿水平方向。质量m=1.0kg的滑块（可视为质点）在水平恒力F=10.0N的作用下，从A点由静止开始运动，当滑块运动的位移x=0.50m时撤去力F。已知A、B之间的距离x0=1.0m，滑块与水平轨道间的动摩擦因数μ=0.10，取g=10m/s2。求：
（1）在撤去力F时，滑块的速度大小；
（2）滑块通过B点时的动能；
（3）滑块通过B点后，能沿圆弧轨道上升的最大高度h=0.35m，求滑块沿圆弧轨道上升过程中克服摩擦力做的功。
（1）
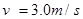（2）
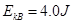（3）
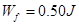
解析试题分析：（1）滑动摩擦力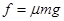
（1分）
设滑块的加速度为a1，根据牛顿第二定律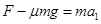
（1分）
解得
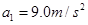（1分）
设滑块运动位移为
时的速度大小为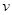
，根据运动学公式
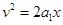（2分）
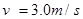解得 （1分）
（2）设滑块通过B点时的动能为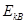
从A到B运动过程中，依据动能定理有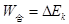
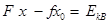， （4分）
解得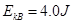 （2分）
（3）设滑块沿圆弧轨道上升过程中克服摩擦力做功为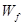
，根据动能定理
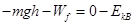（3分）
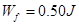解得 （1分）
考点：牛顿运动定律 功能关系
练习册系列答案
金博士一点全通系列答案
相关题目
，AB=CD=2R，A、D等高，D端固定一小挡板，碰撞不损失机械能。滑块的运动始终在包括锅底最低点的竖直平面内，重力加速度为g。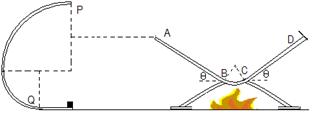
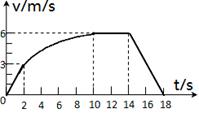
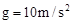，结果保留2位有效数字）。
kx2（k为弹簧的劲度系数，x为弹簧的形变量）．
