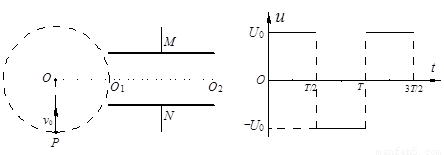题目内容
在真空中,半径为r=3×10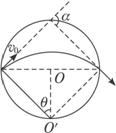
图
(1)粒子在磁场中做匀速圆周运动的半径是多少?
(2)若要使粒子飞离磁场时有最大偏转角,求入射时v0方向与ab的夹角θ及粒子的最大偏转角α.
解析:(1)粒子射入磁场后,由于不计重力,所以洛伦兹力充当圆周运动需要的向心力,根据牛顿第二定律有:qvB=![]() 所以R=
所以R=![]() =5×10
=5×10
(2)粒子在圆形磁场区域轨迹为一段半径R=

图
sinθ=![]() =0.6
=0.6
所以θ=37°
而最大偏转角α=2θ=74°.
答案:(1)R=5×10
(2)θ=37° α=74°

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 (2010?南昌一模)在真空中,半径为r的圆形区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B,在此区域外围空间有垂直纸面向内的磁感应强度大小也为B的匀强磁场.一个带电粒子从边界上的P点沿半径向外,以速度v0进入外围磁场,已知带电粒子质量m=2×10-10kg,带电荷量q=+5×10-6 C,不计重力,磁感应强度B=1T,粒子运动速度v0=5×103 m/s,圆形区域半径r=0.2m,求粒子第一次回到P点所需时间.(结果用π表示)
(2010?南昌一模)在真空中,半径为r的圆形区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B,在此区域外围空间有垂直纸面向内的磁感应强度大小也为B的匀强磁场.一个带电粒子从边界上的P点沿半径向外,以速度v0进入外围磁场,已知带电粒子质量m=2×10-10kg,带电荷量q=+5×10-6 C,不计重力,磁感应强度B=1T,粒子运动速度v0=5×103 m/s,圆形区域半径r=0.2m,求粒子第一次回到P点所需时间.(结果用π表示) (2007?佛山二模)如图所示,在真空中,半径为R=5L0的圆形区域内存在匀强磁场,磁场方向垂直纸面向里.在磁场右侧有一对平行金属板M和N,两板间距离为d=6L0,板长为L=12L0,板的中心线O1O2与磁场的圆心O在同一直线上.给M、N板加上电压U0,其变化情况如下图所示.有一电荷量为q、质量为m的带电的粒子,从M、N板右侧沿板的中心线,在t=0或t=T/4时刻以速率v向左射入M、N之间,粒子在M、N板的左侧刚好以平行于M、N板的速度射出.若上述粒子经磁场后又均能平行于M、N极板返回电场,而电场变化的周期T未知,求磁场磁感应强度B相应必须满足的条件.(不计粒子重力)
(2007?佛山二模)如图所示,在真空中,半径为R=5L0的圆形区域内存在匀强磁场,磁场方向垂直纸面向里.在磁场右侧有一对平行金属板M和N,两板间距离为d=6L0,板长为L=12L0,板的中心线O1O2与磁场的圆心O在同一直线上.给M、N板加上电压U0,其变化情况如下图所示.有一电荷量为q、质量为m的带电的粒子,从M、N板右侧沿板的中心线,在t=0或t=T/4时刻以速率v向左射入M、N之间,粒子在M、N板的左侧刚好以平行于M、N板的速度射出.若上述粒子经磁场后又均能平行于M、N极板返回电场,而电场变化的周期T未知,求磁场磁感应强度B相应必须满足的条件.(不计粒子重力)
 24、.在真空中,半径为R的圆形区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B,在此区域外围空间有垂直纸面向内的大小也为B的磁场,一个带电粒子从边界上的P点沿半径向外,以速度v0进入外围磁场,已知带电粒子质量m=2×10-10kg,带电量q= +5×10-6C,不计重力,磁感应强度B=1T,粒子运动速度v0=5×103m/s,图形区域半径r=0.2m,求粒子第一次回到P点所需时间。
24、.在真空中,半径为R的圆形区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B,在此区域外围空间有垂直纸面向内的大小也为B的磁场,一个带电粒子从边界上的P点沿半径向外,以速度v0进入外围磁场,已知带电粒子质量m=2×10-10kg,带电量q= +5×10-6C,不计重力,磁感应强度B=1T,粒子运动速度v0=5×103m/s,图形区域半径r=0.2m,求粒子第一次回到P点所需时间。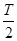 时,将该粒子从MN板右侧沿板的中心线O2O1,仍以速率v0射人M、N之间,求粒子从磁场中射出的点到P点的距离.
时,将该粒子从MN板右侧沿板的中心线O2O1,仍以速率v0射人M、N之间,求粒子从磁场中射出的点到P点的距离.