题目内容
9．
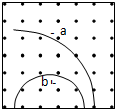如图所示，两个相同的带电粒子，同时垂直射入一个正方形的匀强磁场中做匀速圆周运动，它们的轨迹分别是a和b，则它们的速率和在磁场区域中飞行时间的关系是（ ）| A． | Va＞Vb，ta＞tb | B． | Va＜Vb，ta＜tb | C． | Va＞Vb，ta＜tb | D． | Va=Vb，ta=tb |
分析 通过洛伦兹力提供向心力求出粒子的轨迹半径，再根据粒子的半径大小，比较速度的大小．结合粒子在磁场中运动的周期公式比较两粒子在磁场中的运动时间关系．
解答 解：根据洛伦兹力等于向心力，得：qvB=m$\frac{{v}^{2}}{r}$
则得：r=$\frac{mv}{qB}$
由于a的轨迹半径比b的大，所以有：Va＞Vb．
设轨迹对应的圆心角为θ，则粒子在磁场中的运动时间为：t=$\frac{θ}{2π}$T
粒子运动的周期为：T=$\frac{2πm}{qB}$，可见，周期T相同，由于a的轨迹圆心角小，所以ta＜tb．
故选：C
点评 解决粒子在磁场中圆周运动的基础就是掌握带电粒子在磁场中运动的半径公式和周期公式，并能灵活运用．
练习册系列答案
相关题目
19．下列几种表述中，涉及到的计时数据，指时间间隔的是（ ）
| A． | 刘翔在广州亚运会上110米栏的成绩是13.09s | |
| B． | 2011年9月1日8时全新的高中生活开始 | |
| C． | 中央电视台新闻联播每晚19时开播 | |
| D． | 2013年1月4日，浪漫的日子，你会牵手谁，走上那段红地毯 |
如图所示，带负电的粒子垂直磁场方向进入圆形匀强磁场区域，出磁场时速度偏离原方向60°角，已知带电粒子质量m=3×10-20kg，电量q=10-13C，速度v0=105m/s，磁场区域的半径R=3×10-1m，不计重力，求：
如图所示电路，灯L1标有“24V 16W”灯L2标有“12V 16W”两灯串联后接在电压为U的电路中，要保证两灯不损坏，求：
4．
如图所示，在a点由静止释放一个质量为m，电荷量大小为q的带电粒子，粒子到达b点时速度恰好为零，设ab所在的电场线竖直向下，a、b间的高度差为h，则（ ）
如图所示，在a点由静止释放一个质量为m，电荷量大小为q的带电粒子，粒子到达b点时速度恰好为零，设ab所在的电场线竖直向下，a、b间的高度差为h，则（ ）| A． | 带电粒子带负电 | B． | a、b两点间的电势差Uab=$\frac{mgh}{q}$ | ||
| C． | 带电粒子的机械能保持不变 | D． | a点场强大于b点场强 |
14．
如图所示一质点沿半径为R的圆周运动，在该质点由圆周上的A点运动了$\frac{1}{4}$圆周到达C点的过程中，其位移的大小和路程分别是（ ）
如图所示一质点沿半径为R的圆周运动，在该质点由圆周上的A点运动了$\frac{1}{4}$圆周到达C点的过程中，其位移的大小和路程分别是（ ）| A． | $\frac{\sqrt{2}R}{2}$、πR | B． | R、$\frac{πR}{2}$ | C． | $\sqrt{2}$R、$\frac{πR}{2}$ | D． | $\sqrt{2}$R、πR |
1．元电荷的数值是e=1.6×10-19C，最早是由下列哪位科学家通过实验测得的（ ）
| A． | 密立根 | B． | 库仑 | C． | 安培 | D． | 法拉第 |
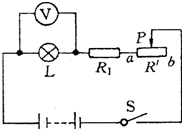如图所示的电路中，电源电压9V，灯泡L的电阻为12Ω，闭合开关后，若要使滑动变阻器滑片P无论如何移动，电压表的示数变化范围总在3～6V之间，求：
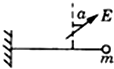如图所示，匀强电场的方向跟竖直方向成a角．在电场中有一质量为m、带电量为q的摆球，当摆线水平时，摆球处于静止．求：