题目内容
如图1所示,长为l、相距为d的两块正对的平行金属板AB和CD与一电源相连(图中未画出电源),B、D为两板的右端点.两板间电压的变化如图2所示.在金属板B、D端的右侧有一与金属板垂直的荧光屏MN,荧光屏距B、D端的距离为l.质量为m、电荷量为 e的电子以相同的初速度v从极板左边中央沿平行极板的直线OO′连续不断地射入.已知所有的电子均能够从金属板间射出,且每个电子在电场中运动的时间与电压变化的周期相等.忽略极板边缘处电场的影响,不计电子的重力以及电子之间的相互作用.求:
(1)t=0和t=T/2时刻进入两板间的电子到达金属板B、D端界面时偏离OO′的距离之比.
(2)两板间电压U的最大值.
(3)电子在荧光屏上分布的最大范围.
【答案】分析:(1)从t=0时刻进入电子先做匀速直线运动,然后做类平抛运动,从t= 时刻进入做类平抛运动,结合牛顿第二定律和运动学公式求出偏转位移,从而求出偏离OO′的距离之比.
时刻进入做类平抛运动,结合牛顿第二定律和运动学公式求出偏转位移,从而求出偏离OO′的距离之比.
(2)在t=(2n+1) (n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离最大,抓住偏转位移小于
(n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离最大,抓住偏转位移小于 ,结合牛顿第二定律和运动学公式求出两板间电压U的最大值.
,结合牛顿第二定律和运动学公式求出两板间电压U的最大值.
(3)分别求出t=(2n+1) (n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离和t=(2n+1)
(n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离和t=(2n+1) (n=0,1,2…)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离,从而确定电子在荧光屏上分布的最大范围.
(n=0,1,2…)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离,从而确定电子在荧光屏上分布的最大范围.
解答:解:(1)t=0时刻进入两板间的电子先沿OO′方向做匀速运动,即有 ,
,
而后在电场力作用下做类平抛运动,在垂直于OO′方向做匀加速运动,设到达B、D
端界面时偏离OO′的距离为y1,则 .
.
t= 时刻进入两板间的电子先在
时刻进入两板间的电子先在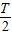 时间内做抛物线运动到达金属板的中央,而后做匀速直线运动到达金属板B、D端界面.设电子到达金属板的中央时偏离OO′的距离为y2,将此时电子的速度分解为沿OO′方向的分量v与沿电场方向的分量vE,并设此时刻电子的速度方向与OO′的夹角为θ,电子沿直线到达金属板B、D端界面时偏离OO′的距离为y2′,则有
时间内做抛物线运动到达金属板的中央,而后做匀速直线运动到达金属板B、D端界面.设电子到达金属板的中央时偏离OO′的距离为y2,将此时电子的速度分解为沿OO′方向的分量v与沿电场方向的分量vE,并设此时刻电子的速度方向与OO′的夹角为θ,电子沿直线到达金属板B、D端界面时偏离OO′的距离为y2′,则有 ,
, ;
;
解得
因此,y1:y2′=1:3.
(2)在t=(2n+1) (n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离最大,因此为使所有进入金属板间的电子都能够飞出金属板,应满足的条件为
(n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离最大,因此为使所有进入金属板间的电子都能够飞出金属板,应满足的条件为 ,解得板间电太的最大值
,解得板间电太的最大值 .
.
(3)设t=nT(n=0,1,2…)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离为Y1;
t=(2n+1) (n=0,1,2…)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离为Y2′,电子到达荧光屏上分布在△Y=Y2-Y1范围内.当满足
(n=0,1,2…)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离为Y2′,电子到达荧光屏上分布在△Y=Y2-Y1范围内.当满足 的条件时,△Y为最大.根据题中金属板和荧光屏之间的几何关系,得到
的条件时,△Y为最大.根据题中金属板和荧光屏之间的几何关系,得到
 .
.
因此电子在荧光屏上分布的最大范围为 .
.
答:(1)t=0和t= 时刻进入两板间的电子到达金属板B、D端界面时偏离OO′的距离之比为1:3.
时刻进入两板间的电子到达金属板B、D端界面时偏离OO′的距离之比为1:3.
(2)两板间电压U的最大值 .
.
(3)电子在荧光屏上分布的最大范围为 .
.
点评:本题考查带电粒子在电场中的偏转,理清粒子的运动规律,结合运动学公式和牛顿第二定律进行求解.
 时刻进入做类平抛运动,结合牛顿第二定律和运动学公式求出偏转位移,从而求出偏离OO′的距离之比.
时刻进入做类平抛运动,结合牛顿第二定律和运动学公式求出偏转位移,从而求出偏离OO′的距离之比.(2)在t=(2n+1)
 (n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离最大,抓住偏转位移小于
(n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离最大,抓住偏转位移小于 ,结合牛顿第二定律和运动学公式求出两板间电压U的最大值.
,结合牛顿第二定律和运动学公式求出两板间电压U的最大值.(3)分别求出t=(2n+1)
 (n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离和t=(2n+1)
(n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离和t=(2n+1) (n=0,1,2…)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离,从而确定电子在荧光屏上分布的最大范围.
(n=0,1,2…)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离,从而确定电子在荧光屏上分布的最大范围.解答:解:(1)t=0时刻进入两板间的电子先沿OO′方向做匀速运动,即有
 ,
,而后在电场力作用下做类平抛运动,在垂直于OO′方向做匀加速运动,设到达B、D
端界面时偏离OO′的距离为y1,则
 .
.t=
 时刻进入两板间的电子先在
时刻进入两板间的电子先在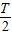 时间内做抛物线运动到达金属板的中央,而后做匀速直线运动到达金属板B、D端界面.设电子到达金属板的中央时偏离OO′的距离为y2,将此时电子的速度分解为沿OO′方向的分量v与沿电场方向的分量vE,并设此时刻电子的速度方向与OO′的夹角为θ,电子沿直线到达金属板B、D端界面时偏离OO′的距离为y2′,则有
时间内做抛物线运动到达金属板的中央,而后做匀速直线运动到达金属板B、D端界面.设电子到达金属板的中央时偏离OO′的距离为y2,将此时电子的速度分解为沿OO′方向的分量v与沿电场方向的分量vE,并设此时刻电子的速度方向与OO′的夹角为θ,电子沿直线到达金属板B、D端界面时偏离OO′的距离为y2′,则有 ,
, ;
;解得

因此,y1:y2′=1:3.
(2)在t=(2n+1)
 (n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离最大,因此为使所有进入金属板间的电子都能够飞出金属板,应满足的条件为
(n=0,1,2…)时刻进入两板间的电子在离开金属板时偏离OO′的距离最大,因此为使所有进入金属板间的电子都能够飞出金属板,应满足的条件为 ,解得板间电太的最大值
,解得板间电太的最大值 .
.(3)设t=nT(n=0,1,2…)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离为Y1;
t=(2n+1)
 (n=0,1,2…)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离为Y2′,电子到达荧光屏上分布在△Y=Y2-Y1范围内.当满足
(n=0,1,2…)时刻进入两板间的电子到达荧光屏上的位置与O′点的距离为Y2′,电子到达荧光屏上分布在△Y=Y2-Y1范围内.当满足 的条件时,△Y为最大.根据题中金属板和荧光屏之间的几何关系,得到
的条件时,△Y为最大.根据题中金属板和荧光屏之间的几何关系,得到 .
.因此电子在荧光屏上分布的最大范围为
 .
.答:(1)t=0和t=
 时刻进入两板间的电子到达金属板B、D端界面时偏离OO′的距离之比为1:3.
时刻进入两板间的电子到达金属板B、D端界面时偏离OO′的距离之比为1:3.(2)两板间电压U的最大值
 .
.(3)电子在荧光屏上分布的最大范围为
 .
.点评:本题考查带电粒子在电场中的偏转,理清粒子的运动规律,结合运动学公式和牛顿第二定律进行求解.

练习册系列答案
相关题目



