题目内容
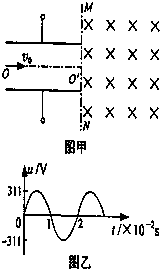
如图(甲)所示,两上下正对水平放置的平行金属板C、D相距很近,上面分别开有小孔O和O′,水平放置的平行金属导轨P、Q与金属板C、D接触良好,且导轨垂直放在磁感强度为B1=10T的竖直向上的匀强磁场中,导轨间距L=0.50m,金属棒AB紧贴着导轨沿平行导轨方向在磁场中做往复运动,其速度图象如图(乙),若规定向右运动速度方向为正方向.从t=0时刻开始,由C板小孔O处连续不断地以垂直于C板方向飘入质量为m=3.2×10-21kg、电量q=1.6×10-19C的带正电的粒子(设飘入速度很小,可视为零).在D板外侧有以MN为边界的匀强磁场B2=10T,方向垂直纸面向里.MN与D相距d=10cm,(粒子重力及其相互作用不计),求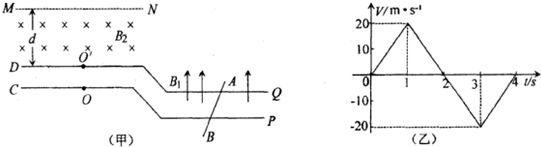
(1)在0到4.0秒内D板电势什么时刻最高?且两板电势差的最大值为多少?
(2)0到4.0秒内哪些时刻从O处飘入的粒子能穿过电场并飞出磁场边界MN?
(3)粒子从边界MN射出来的位置之间最大的距离为多少?

(1)在0到4.0秒内D板电势什么时刻最高?且两板电势差的最大值为多少?
(2)0到4.0秒内哪些时刻从O处飘入的粒子能穿过电场并飞出磁场边界MN?
(3)粒子从边界MN射出来的位置之间最大的距离为多少?
分析:(1)当金属棒沿平行导轨方向在磁场中做往复运动时,产生的感应电动势方向会改变,根据右手定则判断出感应电动势的方向,即可知道D板和C板电势的高低.由E=BLv知,速度最大时,板间的电势差最大.
(2)粒子要飞出磁场边界MN,速度最小时,轨迹半径也最小,恰好与MN相切,可得到轨迹半径为d.根据粒子圆周运动的半径r=
求出粒子进入磁场的速度,即为加速获得的末速度,再由动能定理求出加速电压U,由U=ε=B1Lv 求出AB运动的速度,由乙图可求出所求的量.
(3)当AB棒速度最大,产生的感应电动势最大,CD板间电压最大,粒子经加速得到的速度最大,在磁场中轨迹半径也最大,粒子出MN边时,偏转距离最小,根据法拉第电磁感应定律、动能定理和半径公式结合,并运用几何知识求得粒子从边界MN射出来的位置之间最大的距离.
(2)粒子要飞出磁场边界MN,速度最小时,轨迹半径也最小,恰好与MN相切,可得到轨迹半径为d.根据粒子圆周运动的半径r=
| mv |
| qB |
(3)当AB棒速度最大,产生的感应电动势最大,CD板间电压最大,粒子经加速得到的速度最大,在磁场中轨迹半径也最大,粒子出MN边时,偏转距离最小,根据法拉第电磁感应定律、动能定理和半径公式结合,并运用几何知识求得粒子从边界MN射出来的位置之间最大的距离.
解答:解:(1)根据右手定则判断得知,当金属棒向左运动时,即速度为负值时,D板的电势高于C板的电势.两板电势差等于金属棒所产生的感应电动势,由E=BLv知,速度最大时,板间的电势差最大,所以可知,在3.0秒时刻D板电势最高,为:
U=E=B1Lv=10×0.5×20V=100V
(2)只有当CD板间的电场力方向向上,即AB棒向又运动时,粒子才可能从O运动O′,而粒子飞出磁场边界MN轨迹半径最大为r=d,则粒子能穿过电场并飞出磁场边界MN的最小速度v0必须满足:r=d=
…①
设CD间的电压为U,则有:qU=
m
…②
解①②得:U=25N
又因有:U=?=B1Lv
解得:v0=5m/s.
所以根据(乙)图可以推断在0.25s<t<1.75s内,粒子能穿过CD间的电场,并飞出磁场边界.
(3)当AB棒速度最大,即v′=20m/s时产生感应电动势为:
ε′=B1Lv′=100V
此时带电粒子经加速后速度为v,由动能定理有:
q?′=
mv2
解得:v=
=
=100m/s
此时带电粒子的轨迹半径为:
R′=
=
m=0.2m
出射点与O’的水平距离为:
x=R′-
=(0.2-
)m=0.027m=2.7cm
粒子从边界MN射出来的位置间最大距离为S=d-x=10cm-2.7cm=7.3cm
答:(1)0到4.0s内0.25s<t<1.75s时刻从O处飘入的粒子能穿过电场并飞出磁场边界MN.
(2)粒子从边界MN射出来的位置之间最大的距离为7.3cm
U=E=B1Lv=10×0.5×20V=100V
(2)只有当CD板间的电场力方向向上,即AB棒向又运动时,粒子才可能从O运动O′,而粒子飞出磁场边界MN轨迹半径最大为r=d,则粒子能穿过电场并飞出磁场边界MN的最小速度v0必须满足:r=d=
| mv0 |
| qB2 |
设CD间的电压为U,则有:qU=
| 1 |
| 2 |
| v | 2 0 |
解①②得:U=25N
又因有:U=?=B1Lv
解得:v0=5m/s.
所以根据(乙)图可以推断在0.25s<t<1.75s内,粒子能穿过CD间的电场,并飞出磁场边界.
(3)当AB棒速度最大,即v′=20m/s时产生感应电动势为:
ε′=B1Lv′=100V
此时带电粒子经加速后速度为v,由动能定理有:
q?′=
| 1 |
| 2 |
解得:v=
|
|
此时带电粒子的轨迹半径为:
R′=
| mv |
| qB2 |
| 3.2×10-21×100 |
| 1.6×10-19×10 |
出射点与O’的水平距离为:
x=R′-
| R′2-d2 |
| 0.22-0.12 |
粒子从边界MN射出来的位置间最大距离为S=d-x=10cm-2.7cm=7.3cm
答:(1)0到4.0s内0.25s<t<1.75s时刻从O处飘入的粒子能穿过电场并飞出磁场边界MN.
(2)粒子从边界MN射出来的位置之间最大的距离为7.3cm
点评:本题是电磁感应与带电粒子在磁场中运动的综合,要注意挖掘临界条件,掌握电磁学基本知识和基本的分析思路,属于中档题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目

 如图(甲)所示,两平行金属板间接有如图(乙)所示交变电压u,两板间电场可看作是均匀的,且两板外无电场.已知极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板中线OO′垂直,磁感应强度B=5×10-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷q/m=108C/kg,
如图(甲)所示,两平行金属板间接有如图(乙)所示交变电压u,两板间电场可看作是均匀的,且两板外无电场.已知极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板中线OO′垂直,磁感应强度B=5×10-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷q/m=108C/kg,