题目内容
如图所示,在方向竖直向上、磁感应强度为B的匀强磁场中,有两条相互平行且相距L的光滑金属导轨P1P2P3-Q1Q2Q3,两导轨间用阻值为R的电阻连接,导轨P2P3、Q2Q3在同一水平面上,P2Q2⊥P2P3,倾斜导轨和水平导轨均用相切的一小段光滑圆弧连接,其长度可以略去不计.在倾角为 θ的斜导轨P1P2-Q1Q2上放置一根质量为m的细金属杆AB,杆AB始终垂直于导轨并与导轨保持良好接触.现用沿P1P2方向的拉力F施加于杆AB,使杆AB在高h处由静止开始向下做匀加速直线运动,当杆AB运动到P2Q2处时撤去拉力,最终在CD处停下,测得CD与P2Q2之间的距离为s.不计导轨和杆AB的电阻,不计空气阻力.求:
(1)杆AB下滑的过程中通过电阻R的电荷量q;
(2)杆AB运动到P2Q2处时的速度大小υ
(3)回路中的最大感应电流Im和杆AB在斜导轨上的加速度大小a.

(1)杆AB下滑的过程中通过电阻R的电荷量q;
(2)杆AB运动到P2Q2处时的速度大小υ
(3)回路中的最大感应电流Im和杆AB在斜导轨上的加速度大小a.
分析:(1)杆AB下滑的过程中,可以根据法拉第电磁感应定律、欧姆定律和电量公式q=
?△t求解电量.回路磁通量的变化为:△Ф=B?Lhcotθ.
(2)对AB杆,运用动量定理求解速度v的大小.
(3)当杆AB运动到水平轨道的P2Q2处时,垂直切割磁感线,产生的感应电动势最大,回路中的感应电流最大.根据法拉第定律和欧姆定律求解最大感应电流Im.因杆AB在斜导轨上做匀加速直线运动,可由运动学公式求解加速度a大小.
. |
| I |
(2)对AB杆,运用动量定理求解速度v的大小.
(3)当杆AB运动到水平轨道的P2Q2处时,垂直切割磁感线,产生的感应电动势最大,回路中的感应电流最大.根据法拉第定律和欧姆定律求解最大感应电流Im.因杆AB在斜导轨上做匀加速直线运动,可由运动学公式求解加速度a大小.
解答:解:(1)设杆AB下滑过程中所用的时间为△t.则下滑过程中的平均感应电动势为:
=
…①
平均电流:
=
…②
又 q=
?△t…③
由①②③解得:q=
…④
而△Ф=B?Lhcotθ…⑤
由④⑤可得:q=
…⑥
(2)设杆AB在P2Q2处的速度大小为v.在水平导轨上运动的过程中,由动量定理得:
-B
L?△t′=-mv…⑦
又 q′=
?△t′…⑧
与④式同理可得:q′=
=
…⑨
由⑦⑧⑨解得:v=
(3)杆AB运动到水平轨道的P2Q2处时,回路中的感应电流最大.
感应电动势最大值为:Em=BLv.
则 Im=
=
杆AB在斜导轨上做匀加速直线运动,则有:v2=2a?
.
所以有:a=
=
.
答:(1)杆AB下滑的过程中通过电阻R的电荷量q为
;
(2)杆AB运动到P2Q2处时的速度大小v为
.
(3)回路中的最大感应电流Im为
.杆AB在斜导轨上的加速度大小a为
.
. |
| E |
| △Ф |
| △t |
平均电流:
. |
| I |
| ||
| R |
又 q=
. |
| I |
由①②③解得:q=
| △Ф |
| R |
而△Ф=B?Lhcotθ…⑤
由④⑤可得:q=
| BLhcotθ |
| R |
(2)设杆AB在P2Q2处的速度大小为v.在水平导轨上运动的过程中,由动量定理得:
-B
. |
| I′ |
又 q′=
. |
| I′ |
与④式同理可得:q′=
| △Ф′ |
| R |
| BLs |
| R |
由⑦⑧⑨解得:v=
| B2L2s |
| mR |
(3)杆AB运动到水平轨道的P2Q2处时,回路中的感应电流最大.
感应电动势最大值为:Em=BLv.
则 Im=
| Em |
| R |
| B3L3s |
| mR2 |
杆AB在斜导轨上做匀加速直线运动,则有:v2=2a?
| h |
| sinθ |
所以有:a=
| v2sinθ |
| 2h |
| B4L4s2sinθ |
| 2m2R2h |
答:(1)杆AB下滑的过程中通过电阻R的电荷量q为
| BLhcotθ |
| R |
(2)杆AB运动到P2Q2处时的速度大小v为
| B2L2s |
| mR |
(3)回路中的最大感应电流Im为
| B3L3s |
| mR2 |
| B4L4s2sinθ |
| 2m2R2h |
点评:解决本题时,推导电量的经验公式q=
和运用动量定理求速度是解题的关键,并能抓住感应电荷量与动量定理之间的内在联系.
| △Ф |
| R |

练习册系列答案
相关题目
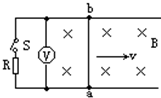 如图所示,在方向竖直向下的磁感强度B=5T的匀强磁场中,水平放置两根间距d=0.1m的平行光滑直导轨,左端接有电阻R=4Ω,以及电键S和电压表(可看作理想电压表).垂直于导轨搁置一根电阻r=1Ω的金属棒ab,棒与导轨良好接触.在电键S闭合前、后一外力均使金属棒以速度v=10m/s匀速向右移动,试求:
如图所示,在方向竖直向下的磁感强度B=5T的匀强磁场中,水平放置两根间距d=0.1m的平行光滑直导轨,左端接有电阻R=4Ω,以及电键S和电压表(可看作理想电压表).垂直于导轨搁置一根电阻r=1Ω的金属棒ab,棒与导轨良好接触.在电键S闭合前、后一外力均使金属棒以速度v=10m/s匀速向右移动,试求: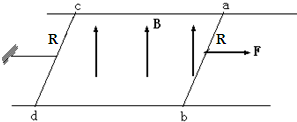 (2009?上海模拟)如图所示,在方向竖直向上、磁感应强度为B的匀强磁场中,有两条光滑的平行金属导轨,其电阻不计,间距为L,导轨平面与磁场方向垂直,ab、cd为垂直放置在导轨上的两根相同的金属棒,它们的电阻都为R、质量都为m,abdca构成闭合回路,cd棒用能承受最大拉力为FT的水平细线拉住,ab棒在水平拉力F的作用下以加速度a由静止开始向右做匀加速运动.
(2009?上海模拟)如图所示,在方向竖直向上、磁感应强度为B的匀强磁场中,有两条光滑的平行金属导轨,其电阻不计,间距为L,导轨平面与磁场方向垂直,ab、cd为垂直放置在导轨上的两根相同的金属棒,它们的电阻都为R、质量都为m,abdca构成闭合回路,cd棒用能承受最大拉力为FT的水平细线拉住,ab棒在水平拉力F的作用下以加速度a由静止开始向右做匀加速运动.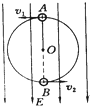 如图所示,在方向竖直向下的匀强电场中,一绝缘轻细线一端固定于O点,另一端系一带正电的小球在竖直平面内做圆周运动.小球的带电量为q,质量为m,绝缘细线长为L,电场的场强为E,若带电小球恰好能通过最高点A,则在A点时小球的速率v1为多大?小球运动到最低点B时的速率v2为多大?运动到B点时细线对小球的拉力为多大?
如图所示,在方向竖直向下的匀强电场中,一绝缘轻细线一端固定于O点,另一端系一带正电的小球在竖直平面内做圆周运动.小球的带电量为q,质量为m,绝缘细线长为L,电场的场强为E,若带电小球恰好能通过最高点A,则在A点时小球的速率v1为多大?小球运动到最低点B时的速率v2为多大?运动到B点时细线对小球的拉力为多大?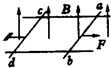 如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中,有两条光滑的平行金属导轨,其电阻不计,间距为L,导轨平面与磁场方向垂直,ab、cd为两根垂直导轨放置的、电阻都为R、质量都为m的金属棒.棒cd用水平细线拉住,棒ab在水平拉力F的作用下以加速度a静止开始向右做匀加速运动,求:
如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中,有两条光滑的平行金属导轨,其电阻不计,间距为L,导轨平面与磁场方向垂直,ab、cd为两根垂直导轨放置的、电阻都为R、质量都为m的金属棒.棒cd用水平细线拉住,棒ab在水平拉力F的作用下以加速度a静止开始向右做匀加速运动,求: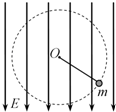 (2005?淮安二模)如图所示,在方向竖直向下的匀强电场中,用绝缘细线拴着带负电的小球(视为质点)在竖直平面内绕O点做圆周运动,则下列判断正确的是( )
(2005?淮安二模)如图所示,在方向竖直向下的匀强电场中,用绝缘细线拴着带负电的小球(视为质点)在竖直平面内绕O点做圆周运动,则下列判断正确的是( )